题目内容
14.若x、y满足约束条件$\left\{\begin{array}{l}{x+y≥1}\\{x-y≥-1}\\{2x-y≤2}\end{array}\right.$,且目标函数z=ax+2y仅在点(1,0)处取得最小值,则a的取值范围是( )| A. | (-1,2) | B. | (-4,2) | C. | (-4,0) | D. | (-2,4) |
分析 若目标函数z=ax+2y仅在点(1,0)处取得最小值,判断目标函数的斜率关系,即可得到结论.
解答 解:作出可行域如图,则直线x+y=1,x-y=-1,2x-y=2的交点分别为A(3,4),B(0,1),C(1,0),
若目标函数z=ax+2y仅在点C(1,0)处取得最小值,
若a=0,则目标函数为z=2y,此时y=$\frac{z}{2}$,满足条件.
若a≠0,则目标函数为y=-$\frac{a}{2}$x+$\frac{z}{2}$,
若a>0,则斜率k=-$\frac{a}{2}$<0,
要使目标函数z=ax+2y仅在点C(1,0)处取得最小值,
则-$\frac{a}{2}$>-1,即a<2,此时0<a<2,
若a<0,则斜率k=-$\frac{a}{2}$>0,
要使目标函数z=ax+2y仅在点C(1,0)处取得最小值,
则-$\frac{a}{2}$<2,即a>-4,此时-4<a<0,
综上-4<a<2,
即a的取值范围(-4,2).
故选:B.
点评 本题主要考查线性规划的应用,根据目标函数的几何意义是解决本题的关键.注意使用数形结合.

练习册系列答案
相关题目
5.设相量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2),若m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,则实数m等于( )
| A. | -$\frac{6}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{10}$ | D. | -$\frac{9}{10}$ |
2.已知点A($\sqrt{3}$,0)和P($\sqrt{3}$,t)(t∈R),若曲线x2+y2=3上存在点B使∠APB=60°,则t的最大值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{3}$ | D. | 3 |
19.在复平面内,复数$\frac{3i}{1-i}$对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.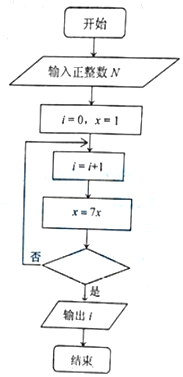 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
3.若变量x,y满足$\left\{\begin{array}{l}{x≤0}\\{y≥0}\\{x-y+1≥0}\end{array}\right.$,则z=x+2y的最大值为( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
4.已知a>b>0,a+b=1,x=-($\frac{1}{a}$)b,y=logab($\frac{1}{a}$+$\frac{1}{b}$),z=logba,则( )
| A. | y<xz | B. | x<z<y | C. | z<y<x | D. | x<y<z |