题目内容
17.已知函数f(x)=2x+2ax(a为实数),且f(1)=$\frac{5}{2}$.(1)求函数f(x)的解析式;
(2)判断函数f(x)的奇偶性并证明;
(3)判断函数f(x)在区间[0,+∞)的单调性,并用定义证明.
分析 (1)根据条件利用待定系数法进行求解即可.
(2)根据函数奇偶性的定义进行证明,
(3)根据函数单调性的定义进行证明即可.
解答 解:(1)∵f(x)=2x+2ax(a为实数),且f(1)=$\frac{5}{2}$.
∴f(1)=2+2a=$\frac{5}{2}$.得2a=$\frac{1}{2}$,即a=-1,
则函数f(x)的解析式f(x)=2x+2-x;
(2)f(-x)=2-x-2x=-(2x-2-x)=-f(x),
则函数f(x)是奇函数.
(3)设0≤x1<x2,f(x1)-f(x2)=${2}^{{x}_{1}}$-$\frac{1}{{2}^{{x}_{1}}}$-${2}^{{x}_{2}}$+$\frac{1}{{2}^{{x}_{2}}}$=(${2}^{{x}_{1}}$-${2}^{{x}_{2}}$)(1+$\frac{1}{{2}^{{x}_{1}+{x}_{2}}}$),
∵y=2x是增函数,∴${2}^{{x}_{1}}$-${2}^{{x}_{2}}$<0,又1+$\frac{1}{{2}^{{x}_{1}+{x}_{2}}}$>0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),函数f(x)是增函数.
点评 本题主要考查函数解析式的求解,以及函数单调性和奇偶性的判断,利用函数奇偶性和单调性的定义是解决本题的关键.

练习册系列答案
相关题目
8.已知向量$\overrightarrow{a}$=(-1,6),$\overrightarrow{b}$=(3,-2),则$\overrightarrow{a}$+$\overrightarrow{b}$=( )
| A. | (4,4) | B. | (2,4) | C. | (-2,4) | D. | (-4,4) |
5.设相量$\overrightarrow{a}$=(2,3),$\overrightarrow{b}$=(-1,2),若m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-2$\overrightarrow{b}$垂直,则实数m等于( )
| A. | -$\frac{6}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{10}$ | D. | -$\frac{9}{10}$ |
2.已知点A($\sqrt{3}$,0)和P($\sqrt{3}$,t)(t∈R),若曲线x2+y2=3上存在点B使∠APB=60°,则t的最大值为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 1+$\sqrt{3}$ | D. | 3 |
6.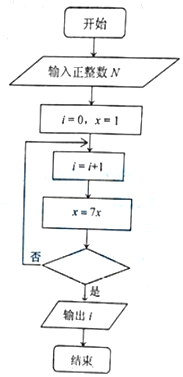 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
7.设实数x,y满足$\left\{\begin{array}{l}{y≤2x-2}\\{x+y-2≥0}\\{x≤2}\end{array}\right.$,则$\frac{y-1}{x+3}$的取值范围是( )
| A. | (-∞,$\frac{1}{5}$] | B. | [-$\frac{1}{5}$,1] | C. | (-$\frac{1}{5}$,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1] |