题目内容

已知函数f(x)=2
3
sin2x+2sinxcosx-
3
(
π
3
≤x≤
11π
24
)．
（1）求函数f（x）的值域；
（2）已知锐角△ABC的两边长分别为函数f（x）的最大值与最小值，且△ABC的外接圆半径为
3
2
4
，求△ABC的面积．
考点：正弦定理的应用,三角函数中的恒等变换应用
专题：计算题,三角函数的求值,解三角形
分析：（1）利用辅助角公式、二倍角公式化简函数，即可求函数f（x）的值域；
（2）不妨设a=
3
，b=2，利用△ABC的外接圆半径为
3
2
4
，求出sinA，sinB，进而求出sinC，即可求△ABC的面积．
解答： 解：（1）f（x）=sin2x-
3
cos2x=2sin（2x-
π
3
），
∵
π
3
≤x≤
11π
24
，
∴
π
3
≤2x-
π
3
≤
7π
12
，
∴
3
2
≤sin（2x-
π
3
）≤1，
∴
3
≤2sin（2x-
π
3
）≤2，
∴函数f（x）的值域为[
3
，2]；
（2）不妨设a=
3
，b=2，
∵△ABC的外接圆半径为
3
2
4
，
∴sinA=
a
2r
=
6
3
，sinB=
b
2r
=
2
2
3
，
∴cosA=
3
3
，cosB=
1
3
，
∴sinC=sin（A+B）=sinAcosB+cosAsinB=
6
3
，
∴S△ABC=
1
2
absinC=
1
2
•
3
•2•
6
3
=
2
．
点评：本题考查利用辅助角公式、二倍角公式化简函数，考查正弦定理，考查三角形面积的计算，属于中档题．
练习册系列答案
相关题目
已知椭圆M、抛物线N的焦点均在x轴上的，且M的中心和M的顶点均为原点O，从每条曲线上取两个点，将其坐标记录于下表中：
x 3 -2 4
2
y -2
3
 0 -4
2
2
（Ⅰ）求M，N的标准方程；
（Ⅱ）已知定点A（1，
1
2
），过原点O作直线l交椭圆M于B，C两点，求△ABC面积的最大值和此时直线l的方程．
如图所示，已知椭圆C1和抛物线C2有公共焦点F（1，0），C1的中心和C2的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C2分别相交于A、B两点．
（Ⅰ）写出抛物线C2的标准方程；
（Ⅱ）求证：以AB为直径的圆过原点；
（Ⅲ）若坐标原点O关于直线l的对称点P在抛物线C2上，直线l与椭圆C1有公共点，求椭圆C1的长轴长的最小值．
已知f（x）=lnx，g（x）=af（x）+f′（x），
（1）求g（x）的单调区间；
（2）当a=1时，
    ①比较g(x)与g(
1
x
)的大小；
    ②是否存在x0＞0，使得|g（x）-g（x0）|＜
1
x
对任意x＞0成立？若存在，求出x0的取值范围；若不存在，请说明理由．
已知f（x）=lnx，g（x）=
x
-
1
x
．
（Ⅰ）当x≥1时，求f（x）-g（x）的最大值；
（Ⅱ）求证：
x
＜
x-1
lnx
＜
x+1
2
，?x＞1恒成立；
（Ⅲ）求证：
n2
2
+
3n
8
＜
n
k=1
1
ln
2k+1
2k-1
＜
n2
2
+
n
2
（n≥2，n∈N）．（参考数据：ln3≈1.1，ln5≈1.6）
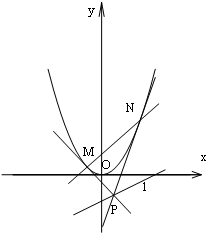已知抛物线C：y=x2，直线l：x-2y-2=0，点P是直线l上任意一点，过点P作抛物线C的切线PM，PN，切点分别为M，N，直线PM，PN斜率分别为k1，k2，如图所示
（1）若P（4，1），求证：k1+k2=16；
（2）若MN过抛物线的焦点，求点P的坐标．
设函数f（x）=|x-1|．若f（a）=2a，则a=
 
．
记曲线y=x2与y=
x
围成的区域为D，若利用计算机产生（0，1）内的两个均匀随机数x，y，则点（x，y）恰好落在区域D内的概率等于
 
．
直线l与双曲线
x2
2
-y2=1的同一支相交于A，B两点，线段AB的中点在直线y=2x上，则直线AB的斜率为（　　）
A、4
B、2
C、
1
2
D、
1
4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网