题目内容
已知函数f(x),当x>0时,f(x)=
.
(1)若函数f(x)在区间(a,a+
)(a>0)上存在极值点,求实数a的取值范围;
(2)若x≥1时,不等式f(x)≥
恒成立,求实数k的取值范围;
(3)试证明:ln(n+1)>n-2 (
+
+
+…+
)(n∈N*)
| 1+lnx |
| x |
(1)若函数f(x)在区间(a,a+
| 1 |
| 3 |
(2)若x≥1时,不等式f(x)≥
| k |
| x+1 |
(3)试证明:ln(n+1)>n-2 (
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的极值
专题:综合题,导数的综合应用
分析:(1)求导函数,确定(x)在(0,1)上单调递增,在(1,+∞)上单调递减,可得函数f(x)在x=1处取得唯一的极值,利用函数f(x)在区间(a,a+
)(a>0)上存在极值点,求实数a的取值范围;
(2)当x≥1时,f(x)≥
恒成立,等价于
≥
恒成立,分离参数可得k≤
,求出右边函数的最小值,即可求实数k的取值范围;
(3)先证明lnx≥1-
>1-
,再令x=
(k=1,2,…,n),即可证明结论.
| 1 |
| 3 |
(2)当x≥1时,f(x)≥
| k |
| x+1 |
| 1+lnx |
| x |
| k |
| x+1 |
| (x+1)(1+lnx) |
| x |
(3)先证明lnx≥1-
| 2 |
| x+1 |
| 2 |
| x |
| k+1 |
| k |
解答:
(1)解:当x>0时,f(x)=
,有f′(x)=-
由f′(x)>0,可得0<x<1;f′(x)<0,可得x>1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴函数f(x)在x=1处取得唯一的极值.
由题意a>0,且a<1<a+
,解得所求实数a的取值范围为
<a<1; …(4分)
(2)解:当x≥1时,f(x)≥
恒成立,等价于
≥
恒成立,
∴k≤
…(5分)
令g(x)=
(x≥1),由题意,k≤g(x)在[1,+∞)上恒成立
g′(x)=
…(6分)
令h(x)=x-lnx(x≥1),则h′(x)=1-
≥0,当且仅当x=1时取等号.
∴h(x)=x-lnx在[1,+∞)上单调递增,
∴h(x)≥h(1)=1>0.…(8分)
∴g′(x)=
>0,
∴g(x)在[1,+∞)上单调递增,
∴g(x)min=g(1)=2.
∴k≤2.
∴所求实数k的取值范围为(-∞,2];…(9分)
(3)证明:由(2),当x≥1时,即f(x)≥
,即
≥
,.…(10分)
从而lnx≥1-
>1-
. …(12分)
令x=
(k=1,2,…,n),得ln
>1-
,ln
>1-
,…,ln
>1-
将以上不等式两端分别相加,
得ln(n+1)>n-2(
+
+
+…+
). …(14分)
| 1+lnx |
| x |
| lnx |
| x2 |
由f′(x)>0,可得0<x<1;f′(x)<0,可得x>1,
∴f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
∴函数f(x)在x=1处取得唯一的极值.
由题意a>0,且a<1<a+
| 1 |
| 3 |
| 2 |
| 3 |
(2)解:当x≥1时,f(x)≥
| k |
| x+1 |
| 1+lnx |
| x |
| k |
| x+1 |
∴k≤
| (x+1)(1+lnx) |
| x |
令g(x)=
| (x+1)(1+lnx) |
| x |
g′(x)=
| x-lnx |
| x2 |
令h(x)=x-lnx(x≥1),则h′(x)=1-
| 1 |
| x |
∴h(x)=x-lnx在[1,+∞)上单调递增,
∴h(x)≥h(1)=1>0.…(8分)
∴g′(x)=
| x-lnx |
| x2 |
∴g(x)在[1,+∞)上单调递增,
∴g(x)min=g(1)=2.
∴k≤2.
∴所求实数k的取值范围为(-∞,2];…(9分)
(3)证明:由(2),当x≥1时,即f(x)≥
| 2 |
| x+1 |
| 1+lnx |
| x |
| 2 |
| x+1 |
从而lnx≥1-
| 2 |
| x+1 |
| 2 |
| x |
令x=
| k+1 |
| k |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2•2 |
| 3 |
| n+1 |
| n |
| 2•n |
| n+1 |
将以上不等式两端分别相加,
得ln(n+1)>n-2(
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| n |
| n+1 |
点评:本题考查导数知识的运用,考查函数的单调性与极值,考查恒成立问题,考查不等式的证明,考查学生分析解决问题的能力,有难度.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
下列函数是奇函数的是( )
| A、f(x)=-|x| |
| B、f(x)=lg(1+x)-lg(1-x) |
| C、f(x)=2x+2-x |
| D、f(x)=x3-1 |
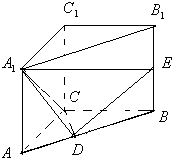 已知直三棱柱ABC-A1B1C1中,∠ACB=
已知直三棱柱ABC-A1B1C1中,∠ACB=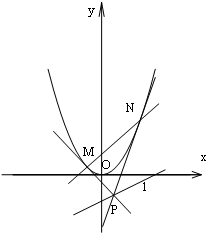 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示