题目内容
若sinx-2cosy=
，cosx+2siny=2，则sin（x-y）= ．
| 2 |
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：将两个式子两边同时平方，然后相加即可得到结论．
解答：
解：由sinx-2cosy=
，cosx+2siny=2，
得（sinx-2cosy）2=2，（cosx+2siny）2=4，
即sin2x-4sinxcosy+4cos2y=2且cos2x+4cosxsiny+4sin2y=4，
两式相加得1+4sin（y-x）+4=2+4=6，
即sin（x-y）=-
，
故答案为：-
；
| 2 |
得（sinx-2cosy）2=2，（cosx+2siny）2=4，
即sin2x-4sinxcosy+4cos2y=2且cos2x+4cosxsiny+4sin2y=4，
两式相加得1+4sin（y-x）+4=2+4=6，
即sin（x-y）=-
| 1 |
| 4 |
故答案为：-
| 1 |
| 4 |
点评：本题主要考查两角和差的正弦公式的应用，利用平方是解决本题的关键．
练习册系列答案
相关题目
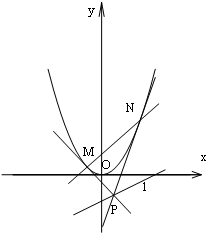已知抛物线C：y=x2，直线l：x-2y-2=0，点P是直线l上任意一点，过点P作抛物线C的切线PM，PN，切点分别为M，N，直线PM，PN斜率分别为k1，k2，如图所示在△ABC中，A=
，BC=
，则“AC=
”是“B=
”的（ ）
| π |
| 4 |
| 2 |
| 3 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |