题目内容
设A、B分别是直线y=±
x上的动点,且|AB|=
,O为坐标原点,若动点P满足
=
+
;动点Q在动圆C1:x2+y2=t2(1<t<4)上.
(1)求动点P的轨迹C2的方程;
(2)若直线PQ与C1和C2均只有一个交点,求线段PQ长度的最大值并求出此时圆C1的方程.
| ||
| 2 |
| 2 |
| OP |
| OA |
| OB |
(1)求动点P的轨迹C2的方程;
(2)若直线PQ与C1和C2均只有一个交点,求线段PQ长度的最大值并求出此时圆C1的方程.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)令A(t,
t),B(s,-
s) p=(x,y),由已知件推导出
,由此能求出动点P的轨迹C2的方程.
(2)若直线PQ的斜率不存在.则|PQ|=0;若直线PQ的斜率存在,设其方程为y=kx+m,P(x1,y2),Q(x2,y2),
联立
,得(4k2+1)x2+8kmx+4(m2-1)=0,由此利用韦达定理和根的判别式能求出|PQ|的最大值和此时圆C1的方程.
| ||
| 2 |
| ||
| 2 |
|
(2)若直线PQ的斜率不存在.则|PQ|=0;若直线PQ的斜率存在,设其方程为y=kx+m,P(x1,y2),Q(x2,y2),
联立
|
解答:
解:(1)令A(t,
t),B(s,-
s)
则p(t+s,
(t-s))=(x,y),
∴
,
而|AB|2=(t-s)2+
(t+s)2=2,
∴(
y)2+
x2=2,
整理,得动点P的轨迹C2的方程为
+y2=1.
(2)若直线PQ的斜率不存在.则|PQ|=0.
若直线PQ的斜率存在,设其方程为y=kx+m,P(x1,y2),Q(x2,y2),
联立
,消去y,并整理,得:
(4k2+1)x2+8kmx+4(m2-1)=0,
∵直线PQ与C1和C2均只有一个交点,
∴△=(8km)2-16(4k2+1)(m2-1)=0,
从而m2=4k2+1,x1=-
,①
又PQ与圆C1相切,得
=t,
∴m2=t2(k2+1),②
由①②得:k2=
,
PQ2=OP2-t2=x12+y12-t2
=x12+1-
-t2
=1+
x12-t2
=1+
-t2
=5-(t2+
)
≤5-4=1.
当且仅当t2=2,即t=
∈(1,4)时取得等号,
∴|PQ|的最大值为1.
此时圆C1的方程x2+y2=1.
| ||
| 2 |
| ||
| 2 |
则p(t+s,
| ||
| 2 |
∴
|
而|AB|2=(t-s)2+
| 1 |
| 2 |
∴(
| 2 |
| 1 |
| 2 |
整理,得动点P的轨迹C2的方程为
| x2 |
| 4 |
(2)若直线PQ的斜率不存在.则|PQ|=0.
若直线PQ的斜率存在,设其方程为y=kx+m,P(x1,y2),Q(x2,y2),
联立
|
(4k2+1)x2+8kmx+4(m2-1)=0,
∵直线PQ与C1和C2均只有一个交点,
∴△=(8km)2-16(4k2+1)(m2-1)=0,
从而m2=4k2+1,x1=-
| 4k |
| m |
又PQ与圆C1相切,得
| |m| | ||
|
∴m2=t2(k2+1),②
由①②得:k2=
| t2-1 |
| 4-t2 |
PQ2=OP2-t2=x12+y12-t2
=x12+1-
| x12 |
| 4 |
=1+
| 3 |
| 4 |
=1+
| 12k2 |
| 4k2+1 |
=5-(t2+
| 4 |
| t2 |
≤5-4=1.
当且仅当t2=2,即t=
| 2 |
∴|PQ|的最大值为1.
此时圆C1的方程x2+y2=1.
点评:本题考查点的轨迹方程的求法,考查线段长的最大值的求法,考查圆的方程的求法,解题时要注意均值定理的合理运用.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
已知不同的直线l,m,不同的平面α,β,下命题中:
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
①若α∥β,l?α,则l∥β
②若α∥β,l⊥α,则l⊥β
③若l∥α,m?α,则l∥m
④若α⊥β,α∩β=l,m⊥l
则真命题的个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
在△ABC中,A=
,BC=
,则“AC=
”是“B=
”的( )
| π |
| 4 |
| 2 |
| 3 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
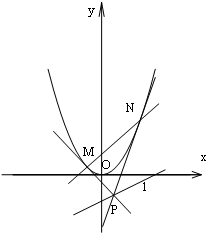 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示