题目内容
已知三点A(2,1),B(1,-2),C(
,-
),动点P(a,b)满足0≤
•
≤2,且0≤
•
≤2,则点P到点C的距离大于
的概率为( )
| 3 |
| 5 |
| 1 |
| 5 |
| OP |
| OA |
| OP |
| OB |
| 1 |
| 5 |
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
考点:几何概型,平面向量数量积的运算
专题:概率与统计
分析:根据向量的数量积的坐标公式将不等式进行化简,作出不等式组对应的平面区域,利用几何概型的概率公式即可得到结论.
解答:
解:∵A(2,1),B(1,-2),C(
,-
),
∴
•
=2a+b,且
•
=a-2b,
∵0≤
•
≤2且0≤
•
≤2,
∴0≤2a+b≤2且0≤a-2b≤2,
作出不等式组对应的平面区域如图:
∵点P到点C的距离大于
,
∴|CP|>
,则对应的部分为阴影部分,
由
解得
,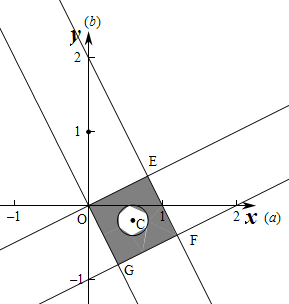
即E(
,
),|OE|=
=
=
,
∴正方形OEFG的面积为
×
=
,
则阴影部分的面积为
-π×(
)2=
-
,
∴根据几何概型的概率公式可知所求的概率为
=1-
,
故选:B.
| 3 |
| 5 |
| 1 |
| 5 |
∴
| OP |
| OA |
| OP |
| OB |
∵0≤
| OP |
| OA |
| OP |
| OB |
∴0≤2a+b≤2且0≤a-2b≤2,
作出不等式组对应的平面区域如图:
∵点P到点C的距离大于
| 1 |
| 5 |
∴|CP|>
| 1 |
| 5 |
由
|
|

即E(
| 4 |
| 5 |
| 2 |
| 5 |
(
|
|
|
∴正方形OEFG的面积为
|
|
| 4 |
| 5 |
则阴影部分的面积为
| 4 |
| 5 |
| 1 |
| 5 |
| 4 |
| 5 |
| π |
| 25 |
∴根据几何概型的概率公式可知所求的概率为
| ||||
|
| π |
| 20 |
故选:B.
点评:本题主要考查几何概型的概率公式的计算,利用数量积将不等式进行转化,求出相应区域的面积是解决本题的关键.

练习册系列答案
相关题目
在△ABC中,A=
,BC=
,则“AC=
”是“B=
”的( )
| π |
| 4 |
| 2 |
| 3 |
| π |
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
直线l与双曲线
-y2=1的同一支相交于A,B两点,线段AB的中点在直线y=2x上,则直线AB的斜率为( )
| x2 |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
D、
|
 执行如图所示的程序框图,若输入值x∈[-2,2],则输出值y的取值范围是( )
执行如图所示的程序框图,若输入值x∈[-2,2],则输出值y的取值范围是( )| A、[-2,1] |
| B、[-2,2] |
| C、[-1,4] |
| D、[-4,1] |
设函数f(x)=
的定义域为M,则∁RM=( )
| 1 | ||
|
| A、(-∞,1) |
| B、(1,+∞) |
| C、(-∞,1] |
| D、[1,+∞) |
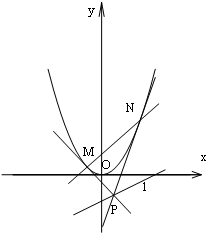 已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示
已知抛物线C:y=x2,直线l:x-2y-2=0,点P是直线l上任意一点,过点P作抛物线C的切线PM,PN,切点分别为M,N,直线PM,PN斜率分别为k1,k2,如图所示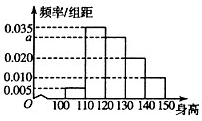 从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[l40,150]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[120,130)的学生中选取的人数应为
从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[l40,150]三组内的学生中,用分层抽样的方法选取30人参加一项活动,则从身高在[120,130)的学生中选取的人数应为