题目内容
已知sinα=
,(0<α<
),求cos(2α-
)的值.
| 1 |
| 3 |
| π |
| 2 |
| π |
| 3 |
考点:二倍角的余弦,二倍角的正弦
专题:计算题,三角函数的求值
分析:由同角三角函数关系式及已知先求cosα,即可求cos2α,sin2α,从而由两角差的余弦公式展开代入即可求值.
解答:
解:∵sinα=
,(0<α<
),
∴cosα=
=
,
∴cos2α=2cos2α-1=
,
sin2α=2sinαcosα=2×
×
=
,
∴cos(2α-
)=cos2αcos
+sin2αsin
,
=
cos2α+
sin2α
=
×
+
×
=
.
| 1 |
| 3 |
| π |
| 2 |
∴cosα=
| 1-sin2α |
2
| ||
| 3 |
∴cos2α=2cos2α-1=
| 7 |
| 9 |
sin2α=2sinαcosα=2×
| 1 |
| 3 |
2
| ||
| 3 |
4
| ||
| 9 |
∴cos(2α-
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
=
| 1 |
| 2 |
| ||
| 2 |
=
| 1 |
| 2 |
| 7 |
| 9 |
| ||
| 2 |
4
| ||
| 9 |
=
7+4
| ||
| 18 |
点评:本题主要考查了同角三角函数关系式的应用,两角差的余弦公式的应用,二倍角的余弦、正弦公式的应用,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,角A,B,C的对边分别是a,b,c,且A,B,C成等差数列,a+c=2,则b的取值范围是( )
| A、[1,2) | ||
| B、(0,2] | ||
C、[1,
| ||
| D、[1,+∞) |
如果tan(α+β)=
,tan(α-
)=
,那么tan(β+
)=( )
| 3 |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
正数a,b满足ab=1,则a+2b的最小值为( )
A、
| ||
B、2
| ||
C、
| ||
| D、3 |
已知等差数列{an}中,a1=1,前10项的和等于前5的和,若am+a6=0,则m=( )
| A、10 | B、9 | C、8 | D、2 |
如图,P、Q是线段AB的三等分点,若
=
,
=
,则
-
=( )
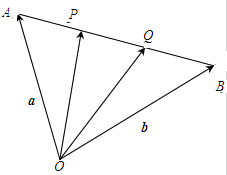
| OA |
| a |
| OB |
| b |
| OP |
| OQ |

A、
| ||||||
B、-
| ||||||
C、
| ||||||
D、-
|
sin240°=( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|