题目内容
等比数列{an}中,a2=2,a5=128.
(1)求数列{an}的通项公式;
(2)令bn=log4an,求数列{bn}的前n项和.
(1)求数列{an}的通项公式;
(2)令bn=log4an,求数列{bn}的前n项和.
考点:数列的求和,等比数列的通项公式
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列的通项公式求出数列的公差,由此能求出an=a2•qn-2=22n-3.
(2)由bn=log422n-3=
,利用等差数列前n项和公式能求出数列{bn}的前n项和.
(2)由bn=log422n-3=
| 2n-3 |
| 2 |
解答:
解:(1)设数列的公差为d,
由a2=2,a5=128,
得a5=a2•q3⇒q3=64⇒q=4,
∴an=a2•qn-2=22n-3.(6分)
(2)∵bn=log4an,
∴bn=log422n-3=
,(10分)
∴Sn=b1+b2+…+bn=
=
.(14分)
由a2=2,a5=128,
得a5=a2•q3⇒q3=64⇒q=4,
∴an=a2•qn-2=22n-3.(6分)
(2)∵bn=log4an,
∴bn=log422n-3=
| 2n-3 |
| 2 |
∴Sn=b1+b2+…+bn=
n[-
| ||||
| 2 |
| n2-2n |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意等差数列的求和公式的合理运用.

练习册系列答案
相关题目
若a=sin2,b=cos2,则a,b的大小为( )
| A、a<b | B、b<a |
| C、a=b | D、不能确定 |
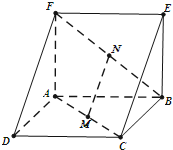 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.