题目内容
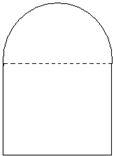 某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?
某建筑设计师设计如图所示的住宅窗户,用长度为p m的铝合金材料做窗框,怎样确定该窗户上半圆的半径和下半矩形的高,才能使窗户的透光,透气功能最好?考点:不等式的实际应用
专题:应用题,函数的性质及应用
分析:下部为矩形,上部为半圆形的框架窗户,设圆的半径为x米,分别计算其面积,可得框架围成的面积y与x的函数式,进一步利用配方法,可求函数的最值.
解答:
解:设圆的半径为x米,框架围成的面积为y,则矩形的一条边为2x米,另一条边为
(p-2x-πx)米,
y=
πx2+
(p-2x-πx)•2x=-(2+
)x2+px=-
(x-
)2+
.
∴该窗户上半圆的半径为
,下半矩形的高
,才能使窗户的透光,透气功能最好.
| 1 |
| 2 |
y=
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| 4+π |
| 2 |
| p |
| π+4 |
| p2 |
| 2π+8 |
∴该窗户上半圆的半径为
| p |
| π+4 |
| p |
| π+4 |
点评:此题考查二次函数的应用,注意利用圆的面积和矩形的面积计算公式建立函数模型解决问题.

练习册系列答案
相关题目
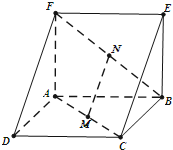 如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.
如图,三棱柱ADF-BCE中,除DF、CE外,其他的棱长均为2,AB⊥AF,平面ABCD⊥平面ABEF,M,N分别是AC,BF上的中点.