题目内容
14.近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)=$\left\{\begin{array}{l}{-0.5{x}^{2}+22x(0≤x≤16)}\\{224(x>16)}\end{array}\right.$,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:(1)求利润函数y=f(x)的解析式(利润=销售收入-总成本);
(2)工厂生产多少百台产品时,可使利润最多?
分析 (1)先求得P(x),再由f(x)=Q(x)-P(x),由分段函数式可得所求;
(2)分别求出各段的最值,注意运用一次函数和二次函数的最值求法,即可得到.
解答 解:(1)由题意得P(x)=12+10x,…(1分)
则f(x)=Q(x)-P(x)=$\left\{\begin{array}{l}{-0.5{x}^{2}+22x-12-10x,0≤x≤16}\\{224-12-10x,x>16}\end{array}\right.$
即为f(x)=$\left\{\begin{array}{l}{-0.5{x}^{2}+12x-12,0≤x≤16}\\{212-10x,x>16}\end{array}\right.$…(4分)
(2)当x>16时,函数f(x)递减,即有f(x)<f(16)=212-160=52万元 …6 分
当0≤x≤16时,函数f(x)=-0.5x2+12x-12
=-0.5(x-12)2+60,
当x=12时,f(x)有最大值60万元.…9 分
所以当工厂生产12百台时,可使利润最大为60万元.…10 分
点评 本题考查函数模型在实际问题中的应用,考查函数的最值问题,正确求出分段函数式,求出各段的最值是解题的关键,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.设全集U={1,2,3,4,5,6},集合A={1,3,5},B={4,5,6},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |
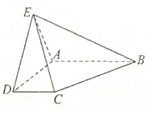 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.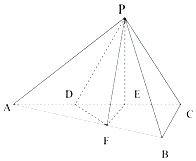 如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.
如图,三棱锥P-ABC中,平面PAC⊥平面ABC,AB⊥BC,点D,E在线段AC上,且AD=DE=EC=2,PD=PC=4,点F在线段AB上,且EF∥平面PBC.