题目内容
4．
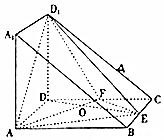将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体，点E，F分别是BC，DC的中点，AF与DE相交于O点．（1）证明：AF⊥平面DD1E；
（2）求三棱锥A-EFD1的体积．
分析 （1）推导出DD1⊥AF，AF⊥DE，由此能证明AF⊥平面DD1E．
（2）三棱锥A-EFD1的体积${V}_{A-EF{D}_{1}}={V}_{{D}_{1}-AEF}$，由此能求出结果．
解答 证明：（1）∵将棱长为2的正方体沿对角A1BAD1截去一半得到如图所示的几何体，
∴D1D⊥平面ABCD，
∵AF?平面ABCD，∴DD1⊥AF，
∵点E，F分别是BC，DC的中点，∴DF=CE，
∵AD=DC，∠ADF=∠DCE=90°，
∴△ADF≌△DCE，∴∠AFD=∠DEC，
∵∠CDE+∠DEC=90°，∴∠CDE+∠AFD=90°，
∴∠DOF=180°-（∠CDE+∠AFD）=90°，∴AF⊥DE，
∵D1D∩DE=D，∴AF⊥平面DD1E．
解：（2）∵D1D⊥平面ABCD，∴D1D是三棱锥D1-AEF的高，且D1D=2，
∵点E，F分别是BC，D1C的中点，∴DF=CF=CE=BE=1，
∴S△AEF=S正方形ABCD-S△ABE-S△ADF-S△CEF=4-$\frac{1}{2}×AB×BE-\frac{1}{2}×AD×DF-\frac{1}{2}×CE×CF$=4-$\frac{1}{2}-1-1$=$\frac{3}{2}$，
∴三棱锥A-EFD1的体积：
${V}_{A-EF{D}_{1}}={V}_{{D}_{1}-AEF}$=$\frac{1}{3}×{S}_{△AEF}×{D}_{1}D$=$\frac{1}{3}×\frac{3}{2}×2=1$．
点评 本题考查直线与平面垂直的证明，棱柱、棱锥、棱台的体积的求法，考查了空间想象能力和推理论证能力，考查了转化思想，属于中档题．
练习册系列答案
相关题目
15．已知函数f（x）=3x，f（a+2）=81，g（x）=$\frac{{1-{a^x}}}{{1+{a^x}}}$．
（1）求g（x）的解析式并判断函数g（x）的奇偶性；
（2）求函数g（x）的值域．
（1）求g（x）的解析式并判断函数g（x）的奇偶性；
（2）求函数g（x）的值域．
12．已知函数y=f（x）（x∈R）且在[0，+∞）上是增函数，g（x）=f（|x|），若g（2x-1）＜g（2），则x的取值范围是（ ）
| A． | （-$\frac{1}{2}$，$\frac{3}{2}$） | B． | （-∞，$\frac{3}{2}$） | C． | （$\frac{3}{2}$，+∞） | D． | （-∞，$-\frac{1}{2}$）∪（$\frac{3}{2}$，+∞） |
9．设全集U={1，2，3，4，5，6}，集合A={1，3，5}，B={4，5，6}，则（∁UA）∩B=（ ）
| A． | {2} | B． | {2，4} | C． | {4，6} | D． | {2，4，6} |
16．函数y=$\sqrt{lo{g}_{5}（1-2sinx）}$，（-$\frac{π}{2}$≤x≤$\frac{π}{2}$）的定义域是（ ）
| A． | [-$\frac{π}{2}$，0] | B． | [-$\frac{π}{2}$，$\frac{π}{6}$） | C． | [-$\frac{π}{2}$，0） | D． | [-$\frac{π}{2}$，$\frac{π}{6}$] |
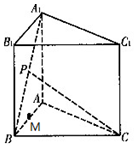已知正三棱柱ABC-A1B1C的各条棱长都为a，P为A1B的中点，M为AB的中点，