题目内容
19.已知函数f(x)=ex-aex(a∈R,e是自然对数的底数).(1)讨论函数f(x)的单调性;
(2)当x∈R时,f(x)≥0恒成立,求a的取值范围.
分析 (1)求出f'(x)=ex-ea,由此利用导数性质能讨论函数f(x)的单调性.
(2)由a<0,a=0,a>0,利用导数性质分类讨论,能求出a的取值范围.
解答 解:(1)由f(x)=ex-eax,得f'(x)=ex-ea.
当a≤0时,f'(x)=ex-ea>0,则f(x)在R上为增函数;
当a>0时,由f'(x)=ex-ea=ex-e1+lna=0,解得x=1+lna.
当x<1+lna时,f'(x)<0;当x>1+lna时,f'(x)>0.
所以f(x)在(-∞,1+lna)上为减函数,
在(1+lna,+∞)上为增函数.
(2)结合(1),得:
当a<0时,设a<-1,则f(2a)=e2x-ea•2a=e2x-2ea2<0,
这与“当x∈R时,f(x)≥0恒成立”矛盾,此时不适合题意.
当a=0时,f(x)=ex,满足“当x∈R时,f(x)≥0恒成立”.
当a>0时,f(x)的极小值点,也是最小值点,
即$f{(x)_{min}}=f(1+lna)={e^{1+lna}}-ea(1+lna)=-ealna$,
由f(x)≥0,得-ealna≥0,解得0<a≤1.
综上,a的取值范围是[0,1].
点评 本题考查函数的单调性的讨论,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
相关题目
10.设抛物线y2=8x的焦点为F,过F作倾斜角为60°的直线交抛物线于A,B两点(点A在第一象限),与其准线交于点C,则$\frac{{S}_{△AOC}}{{S}_{△BOF}}$=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 10 |
9.设全集U={1,2,3,4,5,6},集合A={1,3,5},B={4,5,6},则(∁UA)∩B=( )
| A. | {2} | B. | {2,4} | C. | {4,6} | D. | {2,4,6} |

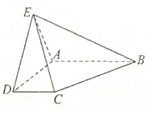 如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.
如图,四棱锥E-ABCD中,底面ABCD为梯形,AB∥CD,且AB=2CD,侧面ADE为等边三角形,侧面ABE为等腰直角三角形,且角A为直角,且平面ABE⊥平面ADE.