题目内容
1．设x＞0，0＜bx＜ax＜1，则正实数a，b的大小关系为（ ）| A． | 1＞a＞b | B． | 1＞b＞a | C． | 1＜a＜b | D． | 1＜b＜a |
分析 根据题意，假设有指数函数y=ax与y=bx，由指数函数的性质可得a＞1且b＞1，又由0＜bx＜ax＜1，则有$\frac{{b}^{x}}{{a}^{x}}$=（$\frac{b}{a}$）x＜1，结合指数函数的性质分析可得a＞b；即可得答案．
解答 解：根据题意，假设有指数函数y=ax与y=bx，
若x＞0，有0＜bx＜ax＜1，
则有a＞1且b＞1，
若0＜bx＜ax＜1，则有$\frac{{b}^{x}}{{a}^{x}}$=（$\frac{b}{a}$）x＜1，
又由x＞0，则$\frac{b}{a}$＜1，即a＞b，
则有1＞a＞b；
故选：A．
点评 本题考查指数函数的图象与性质，关键是掌握指数函数的图象变化的规律．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
12．已知函数y=f（x）（x∈R）且在[0，+∞）上是增函数，g（x）=f（|x|），若g（2x-1）＜g（2），则x的取值范围是（ ）
| A． | （-$\frac{1}{2}$，$\frac{3}{2}$） | B． | （-∞，$\frac{3}{2}$） | C． | （$\frac{3}{2}$，+∞） | D． | （-∞，$-\frac{1}{2}$）∪（$\frac{3}{2}$，+∞） |
9．设全集U={1，2，3，4，5，6}，集合A={1，3，5}，B={4，5，6}，则（∁UA）∩B=（ ）
| A． | {2} | B． | {2，4} | C． | {4，6} | D． | {2，4，6} |
16．函数y=$\sqrt{lo{g}_{5}（1-2sinx）}$，（-$\frac{π}{2}$≤x≤$\frac{π}{2}$）的定义域是（ ）
| A． | [-$\frac{π}{2}$，0] | B． | [-$\frac{π}{2}$，$\frac{π}{6}$） | C． | [-$\frac{π}{2}$，0） | D． | [-$\frac{π}{2}$，$\frac{π}{6}$] |
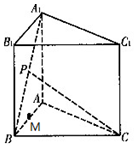已知正三棱柱ABC-A1B1C的各条棱长都为a，P为A1B的中点，M为AB的中点，