题目内容
若直线2x-y+a=0过圆x2+y2-2x+6y=0的圆心，则a的值为（ ）
| A、4 | B、-4 | C、-5 | D、-6 |
考点：直线与圆相交的性质
专题：直线与圆
分析：由已知得圆心（1，-3）在直线2x-y+a=0上，由此能求出a的值．
解答：
解：∵直线2x-y+a=0过圆x2+y2-2x+6y=0的圆心，
∴圆心（1，-3）在直线2x-y+a=0上，
∴2+3+a=0，
解得a=-5．
故选：C
∴圆心（1，-3）在直线2x-y+a=0上，
∴2+3+a=0，
解得a=-5．
故选：C
点评：本题考查实数值的求法，是基础题，解题时要认真审题，注意圆的性质的合理运用．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
二次函数y=x2+ax+b中，若a+b=0，则它的图象必经过点（ ）
| A、（-1，-1） |
| B、（1，-1） |
| C、（1，1） |
| D、（-1，1） |
函数f（x）是R上的偶函数，g（x）是R上的奇函数，满足f（x）+g（x）=(
)x，则有（ ）
| 1 |
| π |
| A、f（2）＜f（3）＜g（0） |
| B、f（2）＜g（0）＜f（3） |
| C、g（0）＜f（2）＜f（3） |
| D、g（0）＜f（3）＜f（2） |
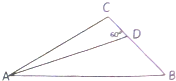爸爸去哪儿节目组安排星娃们露营，村长要求，Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷，AB=8米，BC=4米，AC=6米．现村长给多多一个难题，要求她安扎在B、C两点连线段上的D点位置，∠ADC=60°，如图所示，问多多与Feyman相距多少米？若角A是三角形的一个内角，且sinAcosA＜0，则这个三角形的形状是（ ）
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、等腰直角三角形 |