题目内容
(a+2x+3x2)(1+x)5的展开式中一次项的系数为-3,则x5的系数为 .
考点:二项式系数的性质
专题:二项式定理
分析:依题意,由
a+2=-3可求得a=-1,再由x5的系数为:-1×
+2×
+3×
,计算即可求得答案.
| C | 1 5 |
| C | 5 5 |
| C | 4 5 |
| C | 3 5 |
解答:
解:∵(a+2x+3x2)(1+x)5=(a+2x+3x2)(1+
x+…+
x5),
∴展开式中一次项的系数为
a+2=-3,
解得:a=-1,
∴x5的系数为:-1×
+2×
+3×
=39.
故答案为:39.
| C | 1 5 |
| C | 5 5 |
∴展开式中一次项的系数为
| C | 1 5 |
解得:a=-1,
∴x5的系数为:-1×
| C | 5 5 |
| C | 4 5 |
| C | 3 5 |
故答案为:39.
点评:本题考查二项式系数的性质,求得a=-1是关键,考查运算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
tan1815°+cot
=( )
| 13π |
| 12 |
| A、2 | ||||
| B、2 | ||||
| C、4 | ||||
D、
|
函数f(x)是R上的偶函数,g(x)是R上的奇函数,满足f(x)+g(x)=(
)x,则有( )
| 1 |
| π |
| A、f(2)<f(3)<g(0) |
| B、f(2)<g(0)<f(3) |
| C、g(0)<f(2)<f(3) |
| D、g(0)<f(3)<f(2) |
二次不等式ax2+bx+c<0的解集为{x|x≠-
}的条件为( )
| b |
| 2a |
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
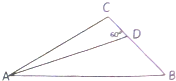 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?