题目内容
对于函数f(x)=
,下列命题正确的是( )
|
| A、值域[-1,1] | ||
B、当且仅当x=2kπ+
| ||
| C、最小正周期为π | ||
D、当且仅当2kπ+π<x<2kπ+
|
考点:四种命题
专题:三角函数的图像与性质
分析:根据题意,讨论函数f(x)的定义域、值域,单调性与最值,从而得出正确的结论.
解答:
解:∵函数f(x)=
,
∴当sinx≥cosx时,
+2kπ≤x≤
+2kπ,
sinx<cosx时,-
+2kπ<x<
+2kπ(k∈Z);
∴f(x)=
,
∴f(x)的值域为[-
,1],A错误;
当x=
+2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1,∴B错误;
∵f(x+π)=
≠f(x),
∴f(x)不是以π为最小正周期的周期函数,∴C错误;
当f(x)<0时,2kπ+π<x<2kπ+
(k∈Z),
又当2kπ+π<x<2kπ+
,(k∈Z)时,f(x)<0,∴D正确;
综上,正确的命题是D.
故选:D.
|
∴当sinx≥cosx时,
| π |
| 4 |
| 5π |
| 4 |
sinx<cosx时,-
| 3π |
| 4 |
| π |
| 4 |
∴f(x)=
|
∴f(x)的值域为[-
| ||
| 2 |
当x=
| π |
| 2 |
∵f(x+π)=
|
∴f(x)不是以π为最小正周期的周期函数,∴C错误;
当f(x)<0时,2kπ+π<x<2kπ+
| 3π |
| 2 |
又当2kπ+π<x<2kπ+
| 3π |
| 2 |
综上,正确的命题是D.
故选:D.
点评:本题考查了三角函数的定义域、值域以及单调性与周期性的应用问题,解题时应熟记三角函数的性质,是中档题.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
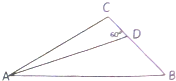 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?