题目内容
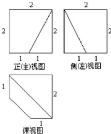
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图知几何体为正方体切去一个棱台,画出其直观图,判断截面为等腰梯形,求出底边长、腰长,再求出梯形的高,代入公式计算可得答案.
解答:
解:由三视图知几何体为正方体切去一个棱台,且切去棱台的下底面直角三角形的直角边长为1,其直观图如图:

∴截面为等腰梯形,且两底边长分别为
,2
,腰长为
,
∴梯形的高为
=
,
∴截面面积S=
×
=
故选C.

∴截面为等腰梯形,且两底边长分别为
| 2 |
| 2 |
| 5 |
∴梯形的高为
(
|
3
| ||
| 2 |
∴截面面积S=
| ||||
| 2 |
3
| ||
| 2 |
| 9 |
| 2 |
故选C.
点评:本题考查了由三视图求几何体的截面积,根据三视图判断几何体的结构特征及求相关几何量的数据是解答本题的关键.

练习册系列答案
相关题目
tan1815°+cot
=( )
| 13π |
| 12 |
| A、2 | ||||
| B、2 | ||||
| C、4 | ||||
D、
|
设集合M={x|x2-2x-3<0},N={x|log2(x-1)≤1},则M∩N等于( )
| A、{x|-1<x<3} |
| B、{x|1<x≤3} |
| C、{x|1<x<3} |
| D、{x|-1≤x≤3} |
函数f(x)是R上的偶函数,g(x)是R上的奇函数,满足f(x)+g(x)=(
)x,则有( )
| 1 |
| π |
| A、f(2)<f(3)<g(0) |
| B、f(2)<g(0)<f(3) |
| C、g(0)<f(2)<f(3) |
| D、g(0)<f(3)<f(2) |
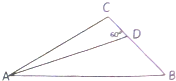 爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?
爸爸去哪儿节目组安排星娃们露营,村长要求,Feyman、杨阳洋、贝儿依次在A、B、C三处扎帐篷,AB=8米,BC=4米,AC=6米.现村长给多多一个难题,要求她安扎在B、C两点连线段上的D点位置,∠ADC=60°,如图所示,问多多与Feyman相距多少米?