题目内容
13.已知函数f(x)=(x-a)e-x,其中a为常数.(1)判断f(x)在x=0处的切线是否经过一个定点,并说明理由;
(2)讨论f(x)在区间[-2,3]上的单调性.
分析 (1)求出函数f(x)的导数,计算f′(0),f(0)的值,求出切线方程,从而求出直线过定点(1,1);
(2)求出函数f(x)的导数,通过讨论a的范围,求出函数的单调区间即可.
解答 解:(1)由题意得f′(x)=$\frac{1+a-x}{{e}^{x}}$,f′(0)=1+a,f(0)=-a,
则在x=0处的切线方程是:y+a=(1+a)x,
即a(x-1)+x-y=0,故定点是(1,1);
(2)由f′(x)=$\frac{1+a-x}{{e}^{x}}$,得f(x)在(-∞,1+a)上递增,在(1+a,+∞)递减,
因此,当1+a≥3即a≥2时,f(x)在[-2,3]递增,
当1+a≤-2即a≤-3时,f(x)在[-2,3]递减,
当-2<1+a<3即-3<a<2时,f(x)在[-2,1+a)递增,在(1+a,3]递减.
点评 本题考查了切线方程问题,考查函数的单调性以及分类讨论思想,是一道中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
3.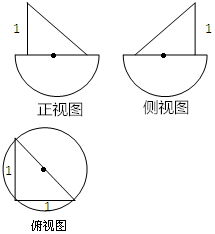 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
 已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )
已知某几何体的三视图如图所示,其中正视图、侧视图均由直角三角形中与半圆构成,俯视图由圆和内接三角形构成,根据图中的数据可得几何体的表面积为( )| A. | 1+$\frac{\sqrt{3}+3π}{2}$ | B. | $\frac{1+\sqrt{3}+π}{2}$ | C. | $\frac{1+\sqrt{3}+3π}{2}$ | D. | $\frac{3+\sqrt{3}+3π}{2}$ |
4.函数$f(x)={(\frac{1}{2})^{\sqrt{x-{x^2}}}}$的单调递增区间为( )
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{0,\frac{1}{2}}]$ | C. | $[\frac{1}{2},+∞)$ | D. | $[{\frac{1}{2},1}]$ |
1.f(x)为奇函数,当x>0时,f(x)=π-arccos(sinx)则x<0时,f(x)=( )
| A. | arccos(sinx) | B. | π+arccos(sinx) | C. | -arccos(sinx) | D. | -π-arccos(sinx) |
18.曲线y=x2-1与直线y=2x+2轴围成的封闭部分的面积为( )
| A. | $\frac{17}{3}$ | B. | $\frac{22}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{35}{3}$ |
5.已知定义在(0,+∞)上的单调函数f(x),对?x∈(0,+∞),都有f[f(x)-lnx]=e+1,则函数g(x)=f(x)-f′(x)-e的零点所在区间是( )
| A. | (1,2) | B. | (2,3) | C. | ($\frac{1}{2}$,1) | D. | (0,$\frac{1}{2}$) |
2.已知直线l与椭圆C:$\frac{x^2}{4}+{y^2}=1$交于A,B两点,且|AB|=2,则直线l与圆x2+y2=1的位置关系为( )
| A. | 相离 | B. | 相交 | C. | 相切 | D. | 相交或相切 |
3.已知球O的半径为R,A,B,C三点在球O的球面上,球心O到平面ABC的距离为$\frac{\sqrt{3}}{2}$R,AB=AC=BC=2$\sqrt{3}$,则球O的表面积为( )
| A. | $\frac{16}{3}$π | B. | 16π | C. | $\frac{64}{3}$π | D. | 64π |