题目内容
3.已知球O的半径为R,A,B,C三点在球O的球面上,球心O到平面ABC的距离为$\frac{\sqrt{3}}{2}$R,AB=AC=BC=2$\sqrt{3}$,则球O的表面积为( )| A. | $\frac{16}{3}$π | B. | 16π | C. | $\frac{64}{3}$π | D. | 64π |
分析 由已知求出截面圆的半径r,根据已知中球心到平面ABC的距离,根据勾股定理求出球的半径,代入球的表面积公式,即可得到答案.
解答 解:设平面ABC截球所得球的小圆半径为r,则2r=$\frac{2\sqrt{3}}{sin60°}$=4,∴r=2,
由${R}^{2}=4+\frac{3}{4}{R}^{2}$得R2=16,所以球的表面积S=4πR2=64π.
故选D.
点评 本题考查的知识点是球的表面积,其中根据球半径,截面圆半径,球心距,构成直角三角形,满足勾股定理,求出球的半径是解答本题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
15.已知四面体A-BCD中,△ABC和△BCD都是边长为6的正三角形,则当四面体的体积最大时,其外接球的表面积是( )
| A. | 60π | B. | 30π | C. | 20π | D. | 15π |
 如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).
如图,一张A4纸的长、宽分别为2$\sqrt{2}$a,2a,A,B,C,D分别是其四条边的中点,现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,关于该多面体的下列命题,正确的是①②③④.(写出所有正确命题的序号).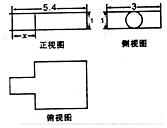 中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )
中国古代数学名著《九章算术》中记载了公元前344年商鞅督造一种标准量器-商鞅铜方升,其三视图如图所示(单位:寸),若π取3,其体积为13.5(立方寸),则图中的x为( )