题目内容

已知x，y为正实数，则（　　）
A、lg（3x+3y）=lg3x+lg3y
B、lg3x+y=lg3x•lg3y
C、lg3xy=lg3x+lg3y
D、lg3x+y=lg3x+lg3y
考点：对数的运算性质
专题：函数的性质及应用
分析：根据对数的运算法则和指数幂的运算法则进行计算即可得到结论．
解答： 解：根据指数幂和对数的运算法则可知lg3x+y=lg3x3y=lg3x+lg3y，
故选：D．
点评：本题主要考查对数和指数幂的运算法则，比较基础．
练习册系列答案
相关题目
设函数f（x）=ln（1+x），g（x）=xf′（x），x≥0，其中f′（x）是f（x）的导函数．
（Ⅰ）令g1（x）=g（x），gn+1（x）=g（gn（x）），n∈N+，求gn（x）的表达式；
（Ⅱ）若f（x）≥ag（x）恒成立，求实数a的取值范围；
（Ⅲ）设n∈N+，比较g（1）+g（2）+…+g（n）与n-f（n）的大小，并加以证明．
若（x+1-y）6的展开式中含x2y3项的系数为a，则a=
 
（用数字作答）．
已知六张卡片中，三张红色，三张黑色，它们分别标有数字2，3，4，打乱后分给甲，乙，丙三人，每人两张，若两张卡片所标数字相同称为“一对”卡片，则三人中至少有一人拿到“一对”卡片的分法数为（　　）
A、18B、24C、42D、48
下列各组函数y=f（x）与y=g（x）在交点处有共同切线的是（　　）
①f（x）=x2-1，g（x）=lnx
②f（x）=3x2+1，g（x）=x3+3x
③f（x）=（x+1）2，g（x）=ex
④f（x）=
x
，g（x）=
e
2
lnx．
A、①②B、②④C、②③D、③④
设函数f（x）=x3-4x+a（a＞0），若f（x）的三个零点分别为x1，x2，x3，且x1＜x2＜x3，则（　　）
A、x1＞-2
B、x12+x22＜
10
3
C、x3＞2
D、x22+x32＜
16
3
已知椭圆C：x2+2y2=4．
（Ⅰ）求椭圆C的离心率；
（Ⅱ）设O为原点，若点A在直线y=2上，点B在椭圆C上，且OA⊥OB，求线段AB长度的最小值．
如图，已知两条抛物线E1：y2=2p1x（p1＞0）和E2：y2=2p2x（p2＞0），过原点O的两条直线l1和l2，l1与E1，E2分别交于A1、A2两点，l2与E1、E2分别交于B1、B2两点．
（Ⅰ）证明：A1B1∥A2B2；
（Ⅱ）过O作直线l（异于l1，l2）与E1、E2分别交于C1、C2两点．记△A1B1C1与△A2B2C2的面积分别为S1与S2，求
S1
S2
的值．
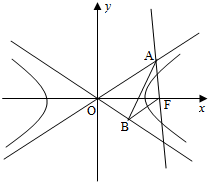如图，已知双曲线C：
x2
a2
-y2=1（a＞0）的右焦点为F，点A，B分别在C的两条渐近线AF⊥x轴，AB⊥OB，BF∥OA（O为坐标原点）．
（1）求双曲线C的方程；
（2）过C上一点P（x0，y0）（y0≠0）的直线l：
x0x
a2
-y0y=1与直线AF相交于点M，与直线x=
3
2
相交于点N．证明：当点P在C上移动时，
丨MF丨
丨NF丨
恒为定值，并求此定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网