题目内容
设函数f(x)=ln(1+x),g(x)=xf′(x),x≥0,其中f′(x)是f(x)的导函数.
(Ⅰ)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式;
(Ⅱ)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(Ⅲ)设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.
(Ⅰ)令g1(x)=g(x),gn+1(x)=g(gn(x)),n∈N+,求gn(x)的表达式;
(Ⅱ)若f(x)≥ag(x)恒成立,求实数a的取值范围;
(Ⅲ)设n∈N+,比较g(1)+g(2)+…+g(n)与n-f(n)的大小,并加以证明.
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知g1(x)=
,g2(x)=g(g1(x))=
=
,g3(x)=
…可得gn(x)=
用数学归纳法加以证明;
(Ⅱ)由已知得到ln(1+x)≥
恒成立构造函数φ(x)=ln(1+x)-
(x≥0),利用导数求出函数的最小值即可;
(Ⅲ)在(Ⅱ)中取a=1,可得ln(1+x)>
,x>0,令x=
则ln
>
,n依次取1,2,3…,然后各式相加即得到不等式.
| x |
| 1+x |
| ||
1+
|
| x |
| 1+2x |
| x |
| 1+3x |
| x |
| 1+nx |
(Ⅱ)由已知得到ln(1+x)≥
| ax |
| 1+x |
| ax |
| 1+x |
(Ⅲ)在(Ⅱ)中取a=1,可得ln(1+x)>
| x |
| 1+x |
| 1 |
| n |
| n+1 |
| n |
| 1 |
| n+1 |
解答:
解:由题设得,g(x)=
(x≥0)
(Ⅰ)由已知g1(x)=
,
g2(x)=g(g1(x))=
=
,
g3(x)=
…
可得gn(x)=
下面用数学归纳法证明.①当n=1时,g1(x)=
,结论成立.
②假设n=k时结论成立,即gk(x)=
,
那么n=k+1时,gk+1(x)=g(gk(x))=
=
=
即结论成立.
由①②可知,结论对n∈N+成立.
(Ⅱ)已知f(x)≥ag(x)恒成立,即ln(1+x)≥
恒成立.
设φ(x)=ln(1+x)-
(x≥0),则φ′(x)=
-
=
,
当a≤1时,φ′(x)≥0(仅当x=0,a=1时取等号成立),
∴φ(x)在[0,+∞)上单调递增,
又φ(0)=0,
∴φ(x)≥0在[0,+∞)上恒成立.
∴当a≤1时,ln(1+x)≥
恒成立,(仅当x=0时等号成立)
当a>1时,对x∈(0,a-1]有φ′(x)<0,∴φ(x)在∈(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0
即当a>1时存在x>0使φ(x)<0,
故知ln(1+x)≥
不恒成立,
综上可知,实数a的取值范围是(-∞,1].
(Ⅲ)由题设知,g(1)+g(2)+…+g(n)=
+
+…+
,
n-f(n)=n-ln(n+1),
比较结果为g(1)+g(2)+…+g(n)>n-ln(n+1)
证明如下:上述不等式等价于
+
+…+
<ln(n+1),
在(Ⅱ)中取a=1,可得ln(1+x)>
,x>0,
令x=
则ln
>
故有ln2-ln1>
,
ln3-ln2>
,…
ln(n+1)-lnn>
,
上述各式相加可得ln(n+1)>
+
+…+
结论得证.
| x |
| 1+x |
(Ⅰ)由已知g1(x)=
| x |
| 1+x |
g2(x)=g(g1(x))=
| ||
1+
|
| x |
| 1+2x |
g3(x)=
| x |
| 1+3x |
可得gn(x)=
| x |
| 1+nx |
下面用数学归纳法证明.①当n=1时,g1(x)=
| x |
| 1+x |
②假设n=k时结论成立,即gk(x)=
| x |
| 1+kx |
那么n=k+1时,gk+1(x)=g(gk(x))=
| gk(x) |
| 1+ gk(x) |
| ||
1+
|
| x |
| 1+(k+1)x |
由①②可知,结论对n∈N+成立.
(Ⅱ)已知f(x)≥ag(x)恒成立,即ln(1+x)≥
| ax |
| 1+x |
设φ(x)=ln(1+x)-
| ax |
| 1+x |
| 1 |
| 1+x |
| a |
| (1+x)2 |
| x+1-a |
| (1+x)2 |
当a≤1时,φ′(x)≥0(仅当x=0,a=1时取等号成立),
∴φ(x)在[0,+∞)上单调递增,
又φ(0)=0,
∴φ(x)≥0在[0,+∞)上恒成立.
∴当a≤1时,ln(1+x)≥
| ax |
| 1+x |
当a>1时,对x∈(0,a-1]有φ′(x)<0,∴φ(x)在∈(0,a-1]上单调递减,
∴φ(a-1)<φ(0)=0
即当a>1时存在x>0使φ(x)<0,
故知ln(1+x)≥
| ax |
| 1+x |
综上可知,实数a的取值范围是(-∞,1].
(Ⅲ)由题设知,g(1)+g(2)+…+g(n)=
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
n-f(n)=n-ln(n+1),
比较结果为g(1)+g(2)+…+g(n)>n-ln(n+1)
证明如下:上述不等式等价于
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
在(Ⅱ)中取a=1,可得ln(1+x)>
| x |
| 1+x |
令x=
| 1 |
| n |
| n+1 |
| n |
| 1 |
| n+1 |
故有ln2-ln1>
| 1 |
| 2 |
ln3-ln2>
| 1 |
| 3 |
ln(n+1)-lnn>
| 1 |
| n+1 |
上述各式相加可得ln(n+1)>
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n+1 |
点评:本题考查数学归纳法;考查构造函数解决不等式问题;考查利用导数求函数的最值,证明不等式,属于一道综合题.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
若实数x、y满足
,则2x-3y的最值情况是( )
|
| A、最大值为2,最小值为-4 |
| B、最大值为2,无最小值 |
| C、无最大值,最小值为-4 |
| D、既无最大值,又无最小值 |
已知x,y为正实数,则( )
| A、lg(3x+3y)=lg3x+lg3y |
| B、lg3x+y=lg3x•lg3y |
| C、lg3xy=lg3x+lg3y |
| D、lg3x+y=lg3x+lg3y |
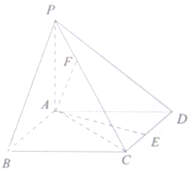 如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.
如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF. 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点. 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2)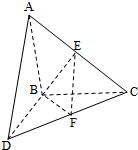 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.