题目内容
已知椭圆C:x2+2y2=4.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设O为原点,若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
(Ⅰ)求椭圆C的离心率;
(Ⅱ)设O为原点,若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
考点:椭圆的简单性质,两点间的距离公式
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(Ⅰ)椭圆C:x2+2y2=4化为标准方程为
+
=1,求出a,c,即可求椭圆C的离心率;
(Ⅱ)先表示出线段AB长度,再利用基本不等式,求出最小值.
| x2 |
| 4 |
| y2 |
| 2 |
(Ⅱ)先表示出线段AB长度,再利用基本不等式,求出最小值.
解答:
解:(Ⅰ)椭圆C:x2+2y2=4化为标准方程为
+
=1,
∴a=2,b=
,c=
,
∴椭圆C的离心率e=
=
;
(Ⅱ)设A(t,2),B(x0,y0),x0≠0,则
∵OA⊥OB,
∴
•
=0,
∴tx0+2y0=0,∴t=-
,
∵x02+2y02=4,
∴|AB|2=(x0-t)2+(y0-2)2=(x0+
)2+(y0-2)2=x02+y02+
+4=x02+
+
+4=
+
+4(0<x02≤4),
因为
+
≥4(0<x02≤4),当且仅当
=
,即x02=4时等号成立,所以|AB|2≥8.
∴线段AB长度的最小值为2
.
| x2 |
| 4 |
| y2 |
| 2 |
∴a=2,b=
| 2 |
| 2 |
∴椭圆C的离心率e=
| c |
| a |
| ||
| 2 |
(Ⅱ)设A(t,2),B(x0,y0),x0≠0,则
∵OA⊥OB,
∴
| OA |
| OB |
∴tx0+2y0=0,∴t=-
| 2y0 |
| x0 |
∵x02+2y02=4,
∴|AB|2=(x0-t)2+(y0-2)2=(x0+
| 2y0 |
| x0 |
| 4y02 |
| x02 |
| 4-x02 |
| 2 |
| 2(4-x02) |
| x02 |
| x02 |
| 2 |
| 8 |
| x02 |
因为
| x02 |
| 2 |
| 8 |
| x02 |
| x02 |
| 2 |
| 8 |
| x02 |
∴线段AB长度的最小值为2
| 2 |
点评:本题考查椭圆的方程与性质,考查基本不等式的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-1上 |
| D、在直线y=x+1上 |
已知x,y为正实数,则( )
| A、lg(3x+3y)=lg3x+lg3y |
| B、lg3x+y=lg3x•lg3y |
| C、lg3xy=lg3x+lg3y |
| D、lg3x+y=lg3x+lg3y |
若复数z=
,其中i为虚数单位,则z的虚部为( )
| 1+i |
| i |
| A、-1 | B、1 | C、i | D、-i |
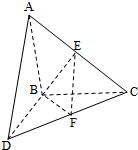 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点. 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+