题目内容
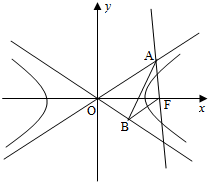 如图,已知双曲线C:
如图,已知双曲线C:| x2 |
| a2 |
(1)求双曲线C的方程;
(2)过C上一点P(x0,y0)(y0≠0)的直线l:
| x0x |
| a2 |
| 3 |
| 2 |
| 丨MF丨 |
| 丨NF丨 |
考点:直线与圆锥曲线的综合问题,直线与圆锥曲线的关系
专题:圆锥曲线的定义、性质与方程
分析:(1)依题意知,A(c,
),设B(t,-
),利用AB⊥OB,BF∥OA,可求得a=
,从而可得双曲线C的方程;
(2)易求A(2,
),l的方程为:
-y0y=1,直线l:
-y0y=1与直线AF相交于点M,与直线x=
相交于点N,可求得M(2,
),N(
,
),于是化简
=
可得其值为
,于是原结论得证.
| c |
| a |
| t |
| a |
| 3 |
(2)易求A(2,
2
| ||
| 3 |
| x0x |
| 3 |
| x0x |
| a2 |
| 3 |
| 2 |
| 2x0-3 |
| 3y0 |
| 3 |
| 2 |
| x0-2 |
| 2y0 |
| 丨MF丨 |
| 丨NF丨 |
|
| ||||||
|
2
| ||
| 3 |
解答:
(1)解:依题意知,A(c,
),设B(t,-
),
∵AB⊥OB,BF∥OA,∴
•
=-1,
=
,
整理得:t=
,a=
,
∴双曲线C的方程为
-y2=1;
(2)证明:由(1)知A(2,
),l的方程为:
-y0y=1,
又F(2,0),直线l:
-y0y=1与直线AF相交于点M,与直线x=
相交于点N.
于是可得M(2,
),N(
,
),
∴
=
=
=
=
=
.
| c |
| a |
| t |
| a |
∵AB⊥OB,BF∥OA,∴
| ||
| c-t |
| -1 |
| a |
| 1 |
| a |
| t |
| a(c-t) |
整理得:t=
| c |
| 2 |
| 3 |
∴双曲线C的方程为
| x2 |
| 3 |
(2)证明:由(1)知A(2,
2
| ||
| 3 |
| x0x |
| 3 |
又F(2,0),直线l:
| x0x |
| a2 |
| 3 |
| 2 |
于是可得M(2,
| 2x0-3 |
| 3y0 |
| 3 |
| 2 |
| x0-2 |
| 2y0 |
∴
| 丨MF丨 |
| 丨NF丨 |
|
| ||||||
|
| 2|2x0-3| | ||
3
|
| 2|2x0-3| | ||||
3
|
| 2|2x0-3| | ||||
3×
|
2
| ||
| 3 |
点评:本题考查直线与圆锥曲线的综合问题,着重考查直线与圆锥曲线的位置关系等基础知识,推理论证能力、运算求解能力、函数与方程思想,属于难题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知x,y为正实数,则( )
| A、lg(3x+3y)=lg3x+lg3y |
| B、lg3x+y=lg3x•lg3y |
| C、lg3xy=lg3x+lg3y |
| D、lg3x+y=lg3x+lg3y |
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
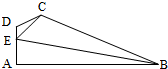 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=