题目内容
下列各组函数y=f(x)与y=g(x)在交点处有共同切线的是( )
①f(x)=x2-1,g(x)=lnx
②f(x)=3x2+1,g(x)=x3+3x
③f(x)=(x+1)2,g(x)=ex
④f(x)=
,g(x)=
lnx.
①f(x)=x2-1,g(x)=lnx
②f(x)=3x2+1,g(x)=x3+3x
③f(x)=(x+1)2,g(x)=ex
④f(x)=
| x |
| e |
| 2 |
| A、①② | B、②④ | C、②③ | D、③④ |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:利用导数的几何意义即可得到切线的斜率及其交点坐标,再判断交点是否相同即可.
解答:
解:①f(x)=x2-1,g(x)=lnx.
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=2x,g′(x)=
(x>0),
若f′(x0)=g′(x0),则2x0=
,解得x0=
.
而f(
)=
-1=-
,g(
)=ln
=-
ln2,
∴f(
)≠g(
),因此不符合条件,应舍去.
②f(x)=3x2-1,g(x)=x3+3x.
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=6x,g′(x)=3x2+3,
若f′(x0)=g′(x0),则6x0=3
+3,解得x0=1.
又f(1)=3+1=4,g(1)=4
∴f(1)=g(1),因此符合条件.
③f(x)=(x+1)2,g(x)=ex.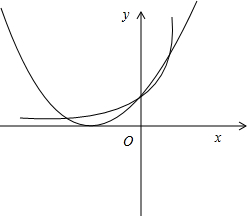
画出图象可知:f(x)与g(x)有三个交点,只有在x=0处的切线相同,
因此不符合题意应该舍去.
④f(x)=
,g(x)=
lnx..
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=
,g′(x)=
,(x>0)
若f′(x0)=g′(x0),则
=
,解得x0=e2.
而f(e2)=
=e,g(e2)=
lne2=e
∴f(e2)=g(e2),因此符合条件.
综上可知:只有②④满足条件.
故选:B.
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=2x,g′(x)=
| 1 |
| x |
若f′(x0)=g′(x0),则2x0=
| 1 |
| x0 |
| ||
| 2 |
而f(
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴f(
| ||
| 2 |
| ||
| 2 |
②f(x)=3x2-1,g(x)=x3+3x.
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=6x,g′(x)=3x2+3,
若f′(x0)=g′(x0),则6x0=3
| x | 2 0 |
又f(1)=3+1=4,g(1)=4
∴f(1)=g(1),因此符合条件.
③f(x)=(x+1)2,g(x)=ex.

画出图象可知:f(x)与g(x)有三个交点,只有在x=0处的切线相同,
因此不符合题意应该舍去.
④f(x)=
| x |
| e |
| 2 |
设函数y=f(x)与y=g(x)的交点为P(x0,y0).
∵f′(x)=
| 1 | ||
2
|
| e |
| 2x |
若f′(x0)=g′(x0),则
| 1 | ||
2
|
| e |
| 2x |
而f(e2)=
| e2 |
| e |
| 2 |
∴f(e2)=g(e2),因此符合条件.
综上可知:只有②④满足条件.
故选:B.
点评:本题考查了导数的几何意义和切线方程,考查了推理能力和计算能力,属于难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-1上 |
| D、在直线y=x+1上 |
已知底面边长为1,侧棱长为
的正四棱柱的各顶点均在同一球面上,则该球的体积为( )
| 2 |
A、
| ||
| B、4π | ||
| C、2π | ||
D、
|
已知x,y为正实数,则( )
| A、lg(3x+3y)=lg3x+lg3y |
| B、lg3x+y=lg3x•lg3y |
| C、lg3xy=lg3x+lg3y |
| D、lg3x+y=lg3x+lg3y |
若复数z=
,其中i为虚数单位,则z的虚部为( )
| 1+i |
| i |
| A、-1 | B、1 | C、i | D、-i |
 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F、G分别为AC、DC、AD的中点.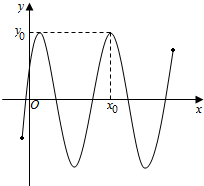 函数f(x)=3sin(2x+
函数f(x)=3sin(2x+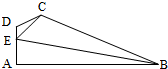 如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=
如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=