题目内容
若(x+1-y)6的展开式中含x2y3项的系数为a,则a= (用数字作答).
考点:二项式系数的性质
专题:二项式定理
分析:展开式中出现含x2y3项,是六个(x+1-y)中,有2个式子出x,三个式子出-y,剩下的一个式子出1,据乘法原理求出a的值.
解答:
解:据乘法原理,展开式中出现含x2y3项,是六个(x+1-y)中,有2个式子出x,三个式子出-y,剩下的一个式子出1,
所以展开式中含x2y3项的系数为a=
•
•(-1)=-60,
故答案为:-60.
所以展开式中含x2y3项的系数为a=
| C | 2 6 |
| C | 3 4 |
故答案为:-60.
点评:本题考查计数原理中的乘法原理,是常见的一种计数方法,属于一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
曲线
(θ为参数)的对称中心( )
|
| A、在直线y=2x上 |
| B、在直线y=-2x上 |
| C、在直线y=x-1上 |
| D、在直线y=x+1上 |
已知x,y为正实数,则( )
| A、lg(3x+3y)=lg3x+lg3y |
| B、lg3x+y=lg3x•lg3y |
| C、lg3xy=lg3x+lg3y |
| D、lg3x+y=lg3x+lg3y |
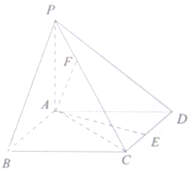 如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.
如图,已知四棱锥,底面ABCD为菱形,PA⊥平面ABCD,PA=AB=2,∠ABC=60°,E是CD的中点,F为PC上一点,满足FC=2PF.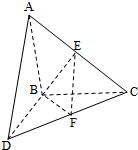 如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.
如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2.∠ABC=∠DBC=120°,E、F分别为AC、DC的中点.