题目内容
已知sin(α-π)=2cos(2π-α),求
的值.
| sin(π-α)+5cos(2π-α) |
| 3cos(π-α)-sin(-α) |
考点:三角函数的化简求值,任意角的概念
专题:计算题,三角函数的求值
分析:通过已知条件求出sinα与cosα的关系,利用诱导公式化简所求表达式,代入求值即可.
解答:
解:∵sin(α-π)=2cos(2π-α),
∴sinα=-2cosα,
∴
=
=
=
.
故答案为:
.
∴sinα=-2cosα,
∴
| csin(π-α)+5cos(2π-α) |
| 3cos(π-α)-sin(-α) |
| sinα-5cosα |
| -3cosα+sinα |
| -2cosα-5cosα |
| -3cosα-2cosα |
| 7 |
| 5 |
故答案为:
| 7 |
| 5 |
点评:本题考查三角函数的化简求值,诱导公式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,既是奇函数又在区间(0,+∞)上单调递增的是( )
A、y=x+
| ||
| B、y=ex-e-x | ||
| C、y=x3-x | ||
| D、y=xlnx |
设x、y满足不等式组
,则x2+y2的最小值为( )
|
| A、1 | ||||
| B、5 | ||||
C、
| ||||
D、
|
两圆x2+y2-4x+6y=0和x2+y2-6x=0的连心线方程为( )
| A、x+y+3=0 |
| B、2x-y-5=0 |
| C、3x-y-9=0 |
| D、4x-3y+7=0 |
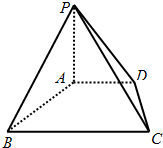 已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为
已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为