题目内容
已知f(x)是R上的减函数,A(3,-1),B(0,1)是其图象上两个点,则不等式|f(1+lnx)|<1的解集是 .
考点:其他不等式的解法,函数单调性的性质
专题:函数的性质及应用
分析:由不等式|f(1+lnx)|<1,利用绝对值的意义可得-1<f(1+lnx)<1,(*)由于A(3,-1),B(0,1)是其图象上两个点,可得f(3)=-1,f(0)=1,因此(*)可化为f(3)<f(1+lnx)<f(0),再利用f(x)是R上的减函数,可得3>1+lnx>0,解出即可.
解答:
解:∵不等式|f(1+lnx)|<1,∴-1<f(1+lnx)<1,(*)
∵A(3,-1),B(0,1)是其图象上两个点,∴f(3)=-1,f(0)=1,
∴(*)可化为f(3)<f(1+lnx)<f(0),
∵f(x)是R上的减函数,∴3>1+lnx>0,化为2>lnx>-1,解得
<x<e2.
∴不等式|f(1+lnx)|<1的解集是(
,e2).
故答案为(
,e2).
∵A(3,-1),B(0,1)是其图象上两个点,∴f(3)=-1,f(0)=1,
∴(*)可化为f(3)<f(1+lnx)<f(0),
∵f(x)是R上的减函数,∴3>1+lnx>0,化为2>lnx>-1,解得
| 1 |
| e |
∴不等式|f(1+lnx)|<1的解集是(
| 1 |
| e |
故答案为(
| 1 |
| e |
点评:本题考查了绝对值不等式、函数的单调性及对数函数的单调性,属于中档题.

练习册系列答案
相关题目
已知sinα+cosα=
,且0≤α<π,那么tanα等于( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知圆的方程为:x2+y2-2x+4y+1=0,则其圆心坐标是( )
| A、(-1,2 ) |
| B、(1,-2) |
| C、(-2,1 ) |
| D、(-2,4) |
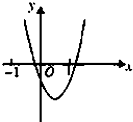 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y=