题目内容
已知a>0,x,y满足
若z=2x+y的最小值为1,则a= .
|
考点:简单线性规划
专题:计算题,不等式的解法及应用
分析:由题意得a>0,作出题中不等式组表示的平面区域,得如图的△ABC及其内部,再将目标函数z=2x+y对应的直线进行平移,可得当x=1且y=-2a时z取得最小值,由此建立关于a的等式,解之即可得到实数a的值.
解答:
解:由题意可得:若可行域不是空集,则直线y=a(x-3)的斜率为正数时.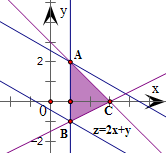
因此a>0,作出不等式组
表示的平面区域,
得到如图的△ABC及其内部,其中A(1,2),B(1,-2a),C(3,0)
设z=F(x,y)=2x+y,将直线l:z=2x+y进行平移,
观察x轴上的截距变化,可得当l经过点B时,目标函数z达到最小值
∴z最小值=F(1,-2a)=1,即2-2a=1,解得a=
故答案为:

因此a>0,作出不等式组
|
得到如图的△ABC及其内部,其中A(1,2),B(1,-2a),C(3,0)
设z=F(x,y)=2x+y,将直线l:z=2x+y进行平移,
观察x轴上的截距变化,可得当l经过点B时,目标函数z达到最小值
∴z最小值=F(1,-2a)=1,即2-2a=1,解得a=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题给出二元一次不等式组,在已知目标函数的最小值情况下求参数a的值,着重考查了二元一次不等式组表示的平面区域和简单的线性规划等知识,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
已知圆的方程为:x2+y2-2x+4y+1=0,则其圆心坐标是( )
| A、(-1,2 ) |
| B、(1,-2) |
| C、(-2,1 ) |
| D、(-2,4) |
已知集合A={x|x2-
x-k=0,x∈(-1,1)},若集合A有且仅有一个元素,则实数k的取值范围是( )
| 3 |
| 2 |
A、(-
| ||||||
B、(
| ||||||
C、[-
| ||||||
D、[-
|
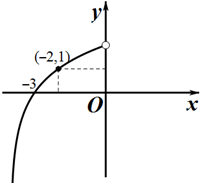 已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.
已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.