题目内容
已知△AOB的面积为1,
=
+
,则△APB的面积为 .
| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 5 |
| OB |
考点:平面向量的基本定理及其意义,三角形的面积公式
专题:平面向量及应用
分析:作PE∥OB,PF∥OA,由
=
+
可得OE=
OA,OF=
OB,可得S△APO=
,S△BPO=
,而S△APB=S△ABO-S△APO-S△BPO,代入化简可得.
| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 5 |
| OB |
| 1 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
解答:
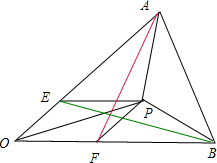 解:如图,作PE∥OB,PF∥OA,
解:如图,作PE∥OB,PF∥OA,
由
=
+
可得OE=
OA,OF=
OB,
∴S△APO=S△AFO=
S△ABO=
,
同理可得S△BPO=S△BEO=
S△ABO=
,
∴△APB的面积S△APB=S△ABO-S△APO-S△BPO=1-
-
=
故答案为:
 解:如图,作PE∥OB,PF∥OA,
解:如图,作PE∥OB,PF∥OA,由
| OP |
| 1 |
| 5 |
| OA |
| 2 |
| 5 |
| OB |
| 1 |
| 5 |
| 2 |
| 5 |
∴S△APO=S△AFO=
| 2 |
| 5 |
| 2 |
| 5 |
同理可得S△BPO=S△BEO=
| 1 |
| 5 |
| 1 |
| 5 |
∴△APB的面积S△APB=S△ABO-S△APO-S△BPO=1-
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
故答案为:
| 2 |
| 5 |
点评:本题考查平面向量基本定理的意义,得出三角形APO与BPO的面积是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
“1,x,9成等比数列”是“x=3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知圆的方程为:x2+y2-2x+4y+1=0,则其圆心坐标是( )
| A、(-1,2 ) |
| B、(1,-2) |
| C、(-2,1 ) |
| D、(-2,4) |
已知集合A={x|x2-
x-k=0,x∈(-1,1)},若集合A有且仅有一个元素,则实数k的取值范围是( )
| 3 |
| 2 |
A、(-
| ||||||
B、(
| ||||||
C、[-
| ||||||
D、[-
|
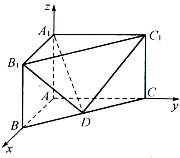 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.