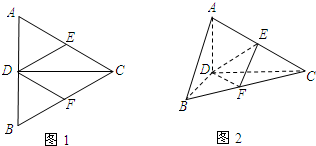
题目内容
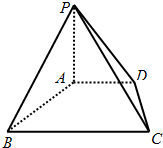 已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为
已知四棱锥P-ABCD的底面ABCD是直角梯形,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AB=BC=2AD,若平面PCD与平面PAB所成二面角的余弦值为
| ||
| 3 |
| PA |
| AD |
考点:用空间向量求平面间的夹角,二面角的平面角及求法
专题:空间角,空间向量及应用
分析:如图所示,建立空间直角坐标系.设PA=t>0,AD=1,则AB=BC=2.则A(0,0,0),B(2,0,0),C(2,2,0),D(0,1,0),P(0,0,t).则
=(-2,-1,0),
=(0,1,-t).求出两个平面的法向量的夹角即可得出.
| CD |
| PD |
解答:
解:如图所示,建立空间直角坐标系.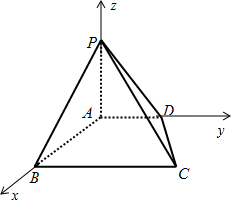
设PA=t>0,AD=1,则AB=BC=2.
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,1,0),P(0,0,t).
则
=(-2,-1,0),
=(0,1,-t).
设平面PCD的法向量为
=(x,y,z).则
,令y=2,则x=-1,z=
.
∴
=(-1,2,
).
取平面PAB的法向量
=(0,1,0).
∴cos<
,
>=
=
=
.
∴
=
,解得t=2.
∴
=2.

设PA=t>0,AD=1,则AB=BC=2.
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,1,0),P(0,0,t).
则
| CD |
| PD |
设平面PCD的法向量为
| m |
|
| 2 |
| t |
∴
| m |
| 2 |
| t |
取平面PAB的法向量
| n |
∴cos<
| m |
| n |
| ||||
|
|
| 2 | ||||
|
| 2 | ||||
|
∴
| 2 | ||||
|
| ||
| 3 |
∴
| PA |
| AD |
点评:本题考查了通过建立空间直角坐标系利用两个平面的法向量的夹角求二面角的方法,属于难题.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
已知
=-2,则
=( )
| lim |
| x→4 |
| f(x)-f(4) |
| x-4 |
| lim |
| t→0 |
| f(4-t)-f(4) |
| 2t |
| A、4 | B、-4 | C、1 | D、-1 |
数列{an}为各项为正数的等比数列,且a4=2,已知函数f(x)=log
x,则f(a13)+f(a23)+…+f(a73)=( )
| 1 |
| 2 |
| A、-6 | B、-21 |
| C、-12 | D、21 |
“1,x,9成等比数列”是“x=3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
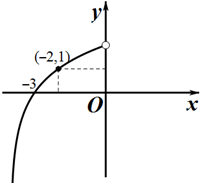 已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.
已知函数f(x)是定义域为R的奇函数.当x<0时,f(x)=loga(x+b),图象如图所示.