题目内容
若a2+b2=
,a-b=
,则a+b的值为 .
| 1 |
| 4 |
| 1 |
| 2 |
考点:直线与圆相交的性质
专题:计算题,函数的性质及应用
分析:利用完全平方公式,将a-b=
平方并代入a2+b2=
,算出2ab=0,从而得出(a+b)2=a2+2ab+b2=a2+b2=
,可得a+b的值.
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
解答:
解:∵a-b=
,
∴(a-b)2=a2-2ab+b2=
.
∵a2+b2=
,
∴(a2+b2)-2ab=
,即
-2ab=
,得2ab=0.
又∵(a+b)2=a2+2ab+b2=a2+b2=
,
∴a+b=±
.
故答案为:±
.
| 1 |
| 2 |
∴(a-b)2=a2-2ab+b2=
| 1 |
| 4 |
∵a2+b2=
| 1 |
| 4 |
∴(a2+b2)-2ab=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
又∵(a+b)2=a2+2ab+b2=a2+b2=
| 1 |
| 4 |
∴a+b=±
| 1 |
| 2 |
故答案为:±
| 1 |
| 2 |
点评:本题给出a、b的平方和与a、b的差,求它们的和.着重考查了完全平方公式和解方程等知识,属于基础题.

练习册系列答案
相关题目
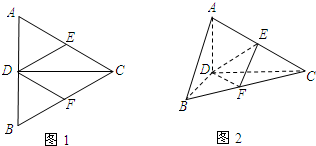
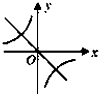
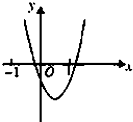 二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
二次函数y=ax2+bx+c的图象如图所示,反比例函数y=
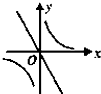
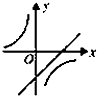
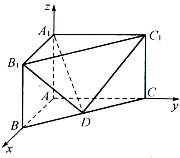 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.