题目内容
设a∈R,若x>0时均有[(a-1)x-1](x2-
x-1)≥0,则a= .
| 3 |
| 2 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:因为x>0,分类讨论,(1)a=1;(2)a≠1,在x>0的整个区间上,我们可以将其分成两个区间,在各自的区间内恒正或恒负,即可得到结论.
解答:
解:(1)a=1时,代入不等式,x>0不等式明显不成立.
(2)a≠1,构造函数y1=(a-1)x-1,y2=(x2-
x-1),它们都过定点P(0,-1).
考查函数y1=(a-1)x-1,令y=0,得M(
,0),因为x>0,不等式成立;
∴a>1;
考查函数y2=x 2-
x-1,因为x>0时均有[(a-1)x-1](x2-
x-1)≥0,显然此函数过点M(
,0),代入得:(
)2-
×
-1=0,
解之得:a=
,或a=0(舍去).
故答案为:
.
(2)a≠1,构造函数y1=(a-1)x-1,y2=(x2-
| 3 |
| 2 |
考查函数y1=(a-1)x-1,令y=0,得M(
| 1 |
| a-1 |
∴a>1;
考查函数y2=x 2-
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| a-1 |
| 1 |
| a-1 |
| 3 |
| 2 |
| 1 |
| a-1 |
解之得:a=
| 3 |
| 2 |
故答案为:
| 3 |
| 2 |
点评:本题考查不等式恒成立问题,解题的关键是构造函数,利用函数的性质求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设函数f(x),g(x)的定义域分别为F,G,且F?G.若对任意的x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”.已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上的一个延拓函数,且g(x)是偶函数,则函数g(x)的解析式是( )
| A、2|x| | ||
| B、log2|x| | ||
C、(
| ||
D、log
|
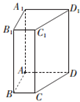 已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4.
已知四棱柱ABCD-A1B1C1D1,侧棱AA1⊥底面ABCD,底面ABCD中,AB⊥AD,BC∥AD,AB=2,AD=4,侧棱AA1=4. 如图,已知AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PA=
如图,已知AB是⊙O的直径,AB=2,C是⊙O上一点,且AC=BC,PA=