题目内容

数列{an}的前n项和为Sn，且Sn=2Sn+1+an2，a2=-1，则数列{an}的首项为（　　）
A、1或-2B、±1
C、±2D、-1或2
考点：数列递推式
专题：
分析：在已知的数列递推式中取n=1，再把a2=-1代入即可得到关于a1的一元二次方程，求解方程得答案．
解答： 解：由Sn=2Sn+1+an2，得
S1=2S2+a12，即a1=2(a1+a2)+a12，
又a2=-1，
∴a12+a1-2=0．
解得：a1=1或-2．
故选：A．
点评：本题考查了数列递推式，考查了一元二次方程的解法，是基础的计算题．
练习册系列答案
相关题目
设a∈R，x∈[-1，1]时，函数y=-x2-ax+b有最小值-1，最大值1，求使函数取得最小值和最大值时相应的x值．
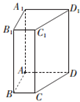已知四棱柱ABCD-A1B1C1D1，侧棱AA1⊥底面ABCD，底面ABCD中，AB⊥AD，BC∥AD，AB=2，AD=4，侧棱AA1=4．
（1）若E是AA1上一点，试确定E点位置使EB∥平面A1CD；
（2）在（1）的条件下，求平面BED与平面ABD所成角的余弦值．
已知函数f（x）=1-
2
3x+1
．
（1）求函数f（x）的定义域，判断并证明f（x）的奇偶性．
（2）用单调性定义证明函数f（x）在其定义域上是增函数；
（3）解不等式f（3m+1）+f（2m-3）＜0．
若函数f（x）在R上是奇函数，且在（-1，0）上单调递增，且f（x+2）=-f（x）．
（1）证明：f（x）的图象关于点（2k，0）中心对称，以及关于直线x=2k+1对称；
（2）讨论f（x）在区间（1，2）上的单调性．
等差数列{an}满足an+an+2+an+4+an+6=8n-48，则nSn的最小值为（　　）
A、-720B、-726
C、11D、12
已知点D（0，
3
），点P在圆C：x2+（y+
3
）2=16上，点，M在DP上，点N在CP上，且DM=MP．MN⊥DP．
（1）求点N的轨迹E的方程；
（2）是否存在点T（0，t），使过点T作圆O：x2+y2=1的切线l交曲线E与A、B两点，△AOB面积S取得最大值，若存在，求出S的最大值和相应的点T的坐标；若不存在，请说明理由．
设f（x）=|x+a|-2x，a＜0，不等式f（x）≤0的解集为M，且M⊆{x|x≥2}．
（1）求实数a的取值范围；
（2）当a取最大值时，求f（x）在[1，10]上的最大值．
已知双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0），过右焦点F的直线与双曲线交于A、B两点，且AB的中点为D（4，2），双曲线的离心率为
3
，则双曲线两焦点的距离等于（　　）
A、7
B、
7
2
C、
4
7
D、
2
7

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网