Question

在△ABC中，∠ACB=2∠ABC，AF、CF分别是△ABC的外角平分线，连接BF，若

AB

AC

=

8

5

，则tan∠AFB的值为

 

．

Answer 1

考点：两角和与差的正切函数

专题：三角函数的求值,解三角形

分析：过F点分别作AB、BC、AC的垂线，垂足分别为D、E、G，则可证明有BF平分∠ABC，故可求得∠AFB=∠ABC，由

AB

AC

=

8

5

可求得cos∠AFB、sin∠AFB的值，从而可求tan∠AFB的值．

解答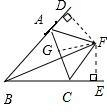： 解：过F点分别作AB、BC、AC的垂线，垂足分别为D、E、G，
∵∠ABC、∠ACB外角的平分线相交于点F，
∴EF=GF，GF=DF，
∴EF=DF，
∴BF平分∠ABC．
若设∠ABC=2x，则有：∠ACB=4x，∠BAC=π-6x，∠FAC=3x，∠ABF=x，故有∠AFB=2x，
在△ABC中，若

AB

AC

=

8

5

，则由正弦定理知：

sin∠ACB

sin∠ABC

=

8

5

⇒

sin4x

sin2x

=

2sin2xcos2x

sin2x

=

8

5

⇒cos2x=cos∠AFB=

4

5

⇒sin∠AFB=

1-cos2∠AFB

=

3

5

，
故有：tan∠AFB=

sin∠AFB

cos∠AFB

=

3

4

．
故答案为：

3

4

．

点评：本题主要考察了正弦定理的应用，考察了数形结合的能力，属于中档题．