题目内容
求函数y=x4-8x3+3（-1≤x≤3）的最大值与最小值．
考点：利用导数求闭区间上函数的最值
专题：函数的性质及应用
分析：由条件利用导数研究函数的单调性，根据函数的单调性求函数的最值．
解答：
解：∵y=x4-8x3+3（-1≤x≤3），∴y′=4x3-24x2=4x2 （x-6），
在（-∞，0）上，y′＜0，y是减函数；在（0，6）上，y′＜0，y是减函数；
在（6，+∞）上，y′＞0，函数y为增函数．
故函数y在[-1，3]上是减函数，故当x=-1时，函数取得最大值为12，
当x=3时，函数取得最小值为-132．
在（-∞，0）上，y′＜0，y是减函数；在（0，6）上，y′＜0，y是减函数；
在（6，+∞）上，y′＞0，函数y为增函数．
故函数y在[-1，3]上是减函数，故当x=-1时，函数取得最大值为12，
当x=3时，函数取得最小值为-132．
点评：本题主要考查利用导数研究函数的单调性，根据函数的单调性求函数的最值，属于基础题．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
已知等差数列{an}的公差和首项都不等于0，且a2、a4、a8成等比数列，则下列式子的值最小的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
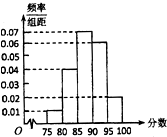某次有1000人参加数学摸底考试，其成绩的频率分布直方图如题（16）图所示，规定85分及以上为优秀．
