题目内容
 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.(Ⅰ)求证:A1B∥平面ADC1;
(Ⅱ)求平面ADC1与ABA1所成二面角的平面角的正弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)连接A1C,交C1A于E,证明:DE∥A1B,即可证明A1B∥平面ADC1;
(Ⅱ)建立空间直角坐标系,求出平面ABA1的一个法向量、平面ADC1的法向量,利用向量的夹角公式,即可求平面ADC1与ABA1所成二面角的平面角的正弦值.
(Ⅱ)建立空间直角坐标系,求出平面ABA1的一个法向量、平面ADC1的法向量,利用向量的夹角公式,即可求平面ADC1与ABA1所成二面角的平面角的正弦值.
解答:
(Ⅰ)证明:连接A1C,交C1A于E,则E为A1C的中点,又点D是BC的中点,
所以DE∥A1B,…(3分)
又DE?平面ADC1,A1B?平面ADC1,故A1B∥平面ADC1. …(5分)
(Ⅱ)解:如图建立空间直角坐标系A-xyz,
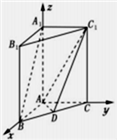
则A(0,0,0),C(0,2,0),D(1,1,0),C1(0,2,4),…(6分)
=(0,2,0)是平面ABA1的一个法向量,…(7分)
设平面ADC1的法向量
=(x,y,z).
∵
=(1,1,0),
=(0,2,4),
∴
.
取z=1,得y=-2,x=2
∴平面ADC1的法向量
=(2,-2,1),…(9分)
平面ADC1与ABA1所成的二面角为θ,
∴|cosθ|=|
|=
.…(11分)
从而sinθ=
,即平面ADC1与ABA1所成二面角的正弦值为
…(13分)
所以DE∥A1B,…(3分)
又DE?平面ADC1,A1B?平面ADC1,故A1B∥平面ADC1. …(5分)
(Ⅱ)解:如图建立空间直角坐标系A-xyz,

则A(0,0,0),C(0,2,0),D(1,1,0),C1(0,2,4),…(6分)
| AC |
设平面ADC1的法向量
| m |
∵
| AD |
| AC1 |
∴
|
取z=1,得y=-2,x=2
∴平面ADC1的法向量
| m |
平面ADC1与ABA1所成的二面角为θ,
∴|cosθ|=|
| -4 |
| 2×3 |
| 2 |
| 3 |
从而sinθ=
| ||
| 3 |
| ||
| 3 |
点评:本题考查线面平行,考查平面ADC1与ABA1所成二面角的正弦值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )
如图,在正方体中,A、B为正方体的两个顶点,M、N、P为所在棱的中点,则异面直线MP、AB在正方体的正视图中的位置关系是( )| A、相交 | B、平行 | C、异面 | D、不确定 |
 如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点
如图,三棱柱ABC-A1B1C1中,侧棱AA⊥底面ABC,且侧棱和底面边长均为2,D是BC的中点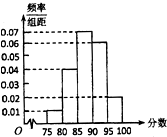 某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
某次有1000人参加数学摸底考试,其成绩的频率分布直方图如题(16)图所示,规定85分及以上为优秀.
