题目内容
设A,B为圆x2+y2=1上两点,O为坐标原点,M为x轴正半轴上一点(A,O,B不共线)
(1)求证:
+
与
-
垂直
(2)当∠MOA=
,∠MOB=θ,θ∈(-
,
),且
•
=
时,求sinθ的值.
(1)求证:
| OA |
| OB |
| OA |
| OB |
(2)当∠MOA=
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| OA |
| OB |
| 3 |
| 5 |
考点:平面向量的综合题
专题:综合题,平面向量及应用
分析:(1)欲证:
+
与
-
垂直,只需证明(
+
)•(
-
)=0即可;
(2)根据
•
=
可求出cos(θ-
)=
,然后根据sinθ=sin[(θ-
)+
],利用正弦的两角和公式进行求解.
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
(2)根据
| OA |
| OB |
| 3 |
| 5 |
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| π |
| 4 |
解答:
(1)证明:由题意知|
|=|
|=1,
∴(
+
)•(
-
)=
2-
2
=|
|2-|
|2=1-1=0,
∴
+
与
-
垂直.
(2)解:
=(cos
,sin
),
=(cosθ,sinθ),
∴
•
=cos
cosθ+sin
sinθ=cos(θ-
),
∵
•
=
,∴cos(θ-
)=
,
∵-
<θ<
,
∴-
<θ-
<0,
∴sin(θ-
)=-
,
∴sinθ=sin[(θ-
)+
]
=sin(θ-
)cos
+cos(θ-
)sin
=-
×
+
×
=-
.
| OA |
| OB |
∴(
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
=|
| OA |
| OB |
∴
| OA |
| OB |
| OA |
| OB |
(2)解:
| OA |
| π |
| 4 |
| π |
| 4 |
| OB |
∴
| OA |
| OB |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
∵
| OA |
| OB |
| 3 |
| 5 |
| π |
| 4 |
| 3 |
| 5 |
∵-
| π |
| 4 |
| π |
| 4 |
∴-
| π |
| 2 |
| π |
| 4 |
∴sin(θ-
| π |
| 4 |
| 4 |
| 5 |
∴sinθ=sin[(θ-
| π |
| 4 |
| π |
| 4 |
=sin(θ-
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=-
| 4 |
| 5 |
| ||
| 2 |
| 3 |
| 5 |
| ||
| 2 |
| ||
| 10 |
点评:本题主要考查了向量在几何中的应用,以及同角三角函数和两角和的正弦公式,同时考查了计算能力,属于中档题.

练习册系列答案
相关题目
一个几何体的三视图及其尺寸如图,则该几何体的表面积为( )


| A、24π | B、15π |
| C、15 | D、24 |
在如图所示的空间直角坐标系O-xyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(2,1,1),(2,2,2).给出编号为①,②,③,④的四个图,则该四面体的侧视图和俯视图分别为( )
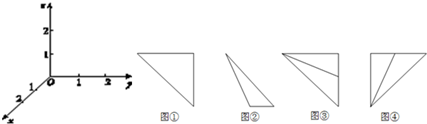

| A、①和② | B、①和③ |
| C、③和② | D、④和② |
若点A是棱长为2的正方体的一个顶点,在这个正方体内随机取一个点P,则点P到点A的距离大于2的概率为( )
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、
|