题目内容
已知集合A={x|-2≤x≤5},B={x|m-1≤x≤m+1}
(1)若m=5,求A∩B
(2)若B⊆A,求实数m的取值范围.
(1)若m=5,求A∩B
(2)若B⊆A,求实数m的取值范围.
考点:交集及其运算,集合的包含关系判断及应用
专题:集合
分析:(1)若m=5,求出集合B,即可求A∩B
(2)若B⊆A,根据集合关系即可求实数m的取值范围.
(2)若B⊆A,根据集合关系即可求实数m的取值范围.
解答:
解:(1)因为m=5,所以B={x|4≤x≤6}.…(1分)
所以A∩B={x|4≤x≤6}…(3分)
(2)易知B≠∅,…(4分)
所以由B⊆A得
…(7分)
得-1≤m≤4…(8分)
所以A∩B={x|4≤x≤6}…(3分)
(2)易知B≠∅,…(4分)
所以由B⊆A得
|
得-1≤m≤4…(8分)
点评:本题主要考查集合的基本运算和集合关系的应用,要求熟练掌握集合的交并补运算,比较基础.

练习册系列答案
相关题目
在△ABC中,角A,B,C的对边分别为a,b,c.已知(a-c)(sinA+sinC)=(b-c)sinB,则角A的大小为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
复数m+(m-3)i是纯虚数,则实数m的值为( )
| A、3 | B、0 | C、2 | D、3或2 |
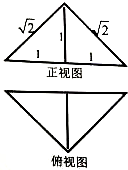 把边长为
把边长为