Question

如图所示的多边形是边长为1的正方形ABCD及以B为圆心，r=1为半径的四分之一圆BOC构成，点P从O点开始沿O→C→D→A运动，设∠OBP=x，记△OBP的面积为f（x），那么函数f（x）的图象是（　　）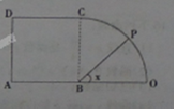

• A、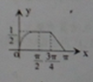
• B、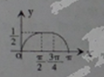
• C、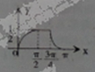
• D、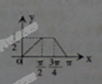

Answer 1

考点：函数的图象

专题：函数的性质及应用

分析：根据三角形的面积公式，讨论点P的位置关系即可得到结论．

解答： 解：若0≤x≤

π

2

，f（x）=

1

2

•xr2=

1

2

x，此时函数对应的图象为线段，
当

π

2

≤x≤

3π

4

，f（x）=

1

2

×OB×1=

1

2

，此时函数为常数，对应的图象为线段，
此时满足条件的图象为D，
故选：D

点评：本题主要考查函数图象的识别和判断，根据条件结合三角形的面积公式是解决本题的关键．