题目内容
若点A是棱长为2的正方体的一个顶点,在这个正方体内随机取一个点P,则点P到点A的距离大于2的概率为( )
A、1-
| ||
B、1-
| ||
C、1-
| ||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:根据题意,分析可得,在正方体ABCD-A1B1C1D1中,与点A距离小于等于2的点在以A为球心,半径为2的八分之一个球内,计算可得其体积,易得正方体的体积;由几何概型公式,可得点P到点A的距离小于等于2的概率,借助对立事件概率的性质,计算可得答案.
解答:
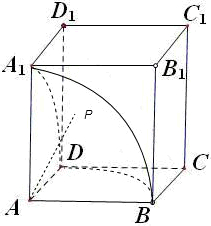 解:根据题意,分析可得,
解:根据题意,分析可得,
在正方体ABCD-A1B1C1D1中,与点A距离小于等于2的点在以A为球心,半径为1的八分之一个球内,
其体积为V1=
×
π×23=
π
正方体的体积为23=8,
则点P到点A的距离小于等于2的概率为:
,
故点P到点A的距离大于2的概率为1-
,
故选:A.
 解:根据题意,分析可得,
解:根据题意,分析可得,在正方体ABCD-A1B1C1D1中,与点A距离小于等于2的点在以A为球心,半径为1的八分之一个球内,
其体积为V1=
| 1 |
| 8 |
| 4 |
| 3 |
| 4 |
| 3 |
正方体的体积为23=8,
则点P到点A的距离小于等于2的概率为:
| π |
| 6 |
故点P到点A的距离大于2的概率为1-
| π |
| 6 |
故选:A.
点评:本题考查几何概型的计算,关键在于掌握正方体的结构特征与正方体、球的体积公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知球的表面积为8π,则它的半径为( )
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |
已知一个三棱锥的正视图和侧视图如图所示,则该三棱锥的俯视图可能为( )


A、 |
B、 |
C、 |
D、 |
关于x与y有如下数据:
有如下的两个模型:①
=0.65x+17.5②
=7x+17,通过残差分析发现第①个线性模型比第②个拟合效果好,则R12 R22,Q1 Q2.(用大于,小于号填空,R,Q分别是相关指数和残差平方和)( )
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
 |
| y |
 |
| y |
| A、<,> | B、>,< |
| C、<,< | D、>,> |
设函数f(x)=kxm,若f(1)=1,f(
)=
,则不等式f(|x|)≤2的解集是( )
| 1 |
| 2 |
| ||
| 2 |
| A、{x|-4≤x≤4} | ||||
| B、{x|0≤x≤4} | ||||
C、{x|-
| ||||
D、{x|0<x≤
|
