题目内容
已知Sn是数列{an}的前n项和,且对任意n∈N*,有4an-3Sn=
(22n+1+1),
(1)求{
}的通项公式;
(2)求数列{
}的前n项和Tn.
| 1 |
| 3 |
(1)求{
| an |
| 4n |
(2)求数列{
| an |
| 2n-2 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)由数列递推式求得a1=3,再由数列递推式得当n≥2时4a n-1-3Sn-1=
(22n-1+1),和原递推式作差得到数列{
}是以
为公差的等差数列,由等差数列的通项公式得答案;
(2)由(1)得
=(2n+1)2n,然后利用错位相减法求其前n项和Tn.
| 1 |
| 3 |
| an |
| 4n |
| 1 |
| 2 |
(2)由(1)得
| an |
| 2n-2 |
解答:
解:(1)当n=1时,4a1-3S1=
(23+1),得a1=3,
当n≥2时,由4a n-3Sn=
(22n+1+1) ①,
得4a n-1-3Sn-1=
(22n-1+1) ②,
①-②得:4a n-4an-1-3an=22n-1,
即an=4an-1+22n-1,化为
=
+
,即
-
=
.
∴数列{
}是以
为首项,以
为公差的等差数列,
则
=
+(n-1)×
=
+
,
=
n+
;
(2)由(1)得:
=(2n+1)2n,
Tn=3•2+5•22+7•23+…+(2n-1)•2n-1+(2n+1)•2n,
2•Tn=3•22+5•23+7•24+…+(2n-1)•2n+(2n+1)•2n+1,
-Tn=6+23+24+…+2n+1-(2n+1)•2n+1,
∴Tn=n•2n+2+1.
| 1 |
| 3 |
当n≥2时,由4a n-3Sn=
| 1 |
| 3 |
得4a n-1-3Sn-1=
| 1 |
| 3 |
①-②得:4a n-4an-1-3an=22n-1,
即an=4an-1+22n-1,化为
| an |
| 4n |
| an-1 |
| 4n-1 |
| 1 |
| 2 |
| an |
| 4n |
| an-1 |
| 4n-1 |
| 1 |
| 2 |
∴数列{
| an |
| 4n |
| 3 |
| 4 |
| 1 |
| 2 |
则
| an |
| 4n |
| 3 |
| 4 |
| 1 |
| 2 |
| n |
| 2 |
| 1 |
| 4 |
| an |
| 4n |
| 1 |
| 2 |
| 1 |
| 4 |
(2)由(1)得:
| an |
| 2n-2 |
Tn=3•2+5•22+7•23+…+(2n-1)•2n-1+(2n+1)•2n,
2•Tn=3•22+5•23+7•24+…+(2n-1)•2n+(2n+1)•2n+1,
-Tn=6+23+24+…+2n+1-(2n+1)•2n+1,
∴Tn=n•2n+2+1.
点评:本题考查了数列递推式,考查了等差关系的确定,训练了错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
已知点A(0,0)、B(2,1)、C(5,5),则向量
在
方向上的投影为( )
| AB |
| AC |
A、
| ||||
B、3
| ||||
C、
| ||||
D、
|
设函数f(x)=kxm,若f(1)=1,f(
)=
,则不等式f(|x|)≤2的解集是( )
| 1 |
| 2 |
| ||
| 2 |
| A、{x|-4≤x≤4} | ||||
| B、{x|0≤x≤4} | ||||
C、{x|-
| ||||
D、{x|0<x≤
|
下列有关命题的说法正确的是( )
| A、命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0” |
| B、命题“若cosx=cosy,则x=y”的逆否命题为真命题 |
| C、若p∧q为假命题,则p,q均为假命题 |
| D、“若x+y=0,则x,y互为相反数”的逆命题为真命题 |
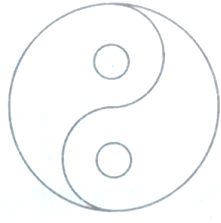 给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有
给如图所示的4个区域涂上颜色,可得一个漂亮的“太极图”,现有红、黑、黄、蓝四种颜色供选用,要求每个区域只能涂一种颜色,且相邻的区域颜色不同,则有