题目内容
若存在实数x满足|x-2|+|x-m|＜5，则实数m的取值范围为 ．
考点：绝对值不等式的解法
专题：计算题,不等式的解法及应用
分析：运用绝对值不等式的性质，可得|x-2|+|x-m|的最小值为|m-2|，由题意可得5＞|m-2|，由绝对值不等式的解法即可得到范围．
解答：
解：由于|x-2|+|x-m|≥|（x-2）-（x-m）|=|m-2|，
则|x-2|+|x-m|的最小值为|m-2|，
由存在实数x满足|x-2|+|x-m|＜5，
则5＞|m-2|，
即为-5＜m-2＜5，
即有-3＜m＜7．
则m的取值范围是（-3，7）．
故答案为：（-3，7）．
则|x-2|+|x-m|的最小值为|m-2|，
由存在实数x满足|x-2|+|x-m|＜5，
则5＞|m-2|，
即为-5＜m-2＜5，
即有-3＜m＜7．
则m的取值范围是（-3，7）．
故答案为：（-3，7）．
点评：本题考查绝对值不等式的解法，考查不等式的存在问题的解法，考查绝对值不等式的性质，属于基础题和易错题．
练习册系列答案
相关题目
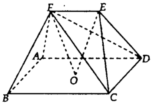如图，O为矩形ABCD的中心，E，F为平面ABCD同侧两点，且EF已知球的表面积为8π，则它的半径为（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
| D、2 |