题目内容
已知等比数列{an}的前n项和Sn=2n+m(m∈R).
(1)求m的值及{an}的通项公式;
(2)设bn=2log2an-13,数列{bn}的前n项和为Tn,求Tn的最小值.
(1)求m的值及{an}的通项公式;
(2)设bn=2log2an-13,数列{bn}的前n项和为Tn,求Tn的最小值.
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件得an=2n+m-2n-1-m=2n-1,由此能求出m.
(2)由bn=2log22n-1-13=2n-15,得{bn}是公差为2的等差数列.由此能求出Tn的最小值.
(2)由bn=2log22n-1-13=2n-15,得{bn}是公差为2的等差数列.由此能求出Tn的最小值.
解答:
解:(1)∵等比数列{an}的前n项和Sn=2n+m(m∈R),
∴an=2n+m-2n-1-m=2n-1…(2分)
∴
=1=2+m,解得m=-1.…(5分)
(2)∵an=2n-1,∴bn=2log22n-1-13=2n-15,
∴{bn}是公差为2的等差数列.
∴Tn=(-13+2n-15)•
=n2-14n
=(n-7)2-49.
∴当n=7时,(Tn)最小值=-49…(10分)
∴an=2n+m-2n-1-m=2n-1…(2分)
∴
| a | 1 |
(2)∵an=2n-1,∴bn=2log22n-1-13=2n-15,
∴{bn}是公差为2的等差数列.
∴Tn=(-13+2n-15)•
| n |
| 2 |
=(n-7)2-49.
∴当n=7时,(Tn)最小值=-49…(10分)
点评:本题考查数列的通项公式的求法,考查前n项和的最小值的求法,解题时要认真审题,注意配方法的合理运用.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
已知函数f(x)=(2m-3)x2+5mx+7为偶函数,则函数f(x)在(1,4)是( )
| A、增函数 |
| B、减函数 |
| C、部分为增函数,部分为减函数 |
| D、无法确定增减性 |
如图:四面体P-ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为( ) 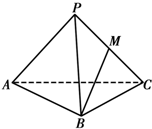

A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
圆x2+y2-2x+2y=0的圆心坐标为( )
| A、(1,-1) |
| B、(1,0) |
| C、(-1,-1) |
| D、(1,1) |
设实数a,b,c满足a+b+c=6,则a,b,c中( )
| A、至多有一个不大于2 |
| B、至少有一个不小于2 |
| C、至多有两个不小于2 |
| D、至少有两个不小于2 |
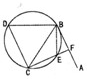 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于E,DB垂直BE交圆于点D. 如图,已知:平行四边形ABCD是矩形,AB=2,BC=1.PD⊥平面ABCD,且PD=3.
如图,已知:平行四边形ABCD是矩形,AB=2,BC=1.PD⊥平面ABCD,且PD=3.