题目内容
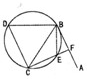 如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于E,DB垂直BE交圆于点D.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于E,DB垂直BE交圆于点D.(1)证明:DB=DC;
(2)设圆的半径为1,BC=
| 3 |
考点:圆內接多边形的性质与判定
专题:选作题,立体几何
分析:(1)连接DE.由于DB垂直BE交圆于点D,可得∠DBE=90°.即DE为圆的直径.由于∠ABC的角平分线BE交圆于点E,利用同圆中的弧圆周角弦之间的关系可得∠DCB=∠DBC,DB=DC.
(II)证明CF⊥AB,DC⊥CF,即可证明DC∥AB.
(II)证明CF⊥AB,DC⊥CF,即可证明DC∥AB.
解答:
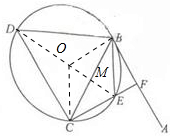 (1)证明:如图所示,连接DE.
(1)证明:如图所示,连接DE.
∵DB垂直BE交圆于点D,∴∠DBE=90°.
∴DE为圆的直径.
∵∠ABC的角平分线BE交圆于点E,
∴
=
,
∴
=
,
∴∠DCB=∠DBC,
∴DB=DC.
(2)解:由(1)可知:∠CDE=∠BDE,DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.
连接OB,OC,则OB⊥AB.
在Rt△BOM中,OB=1,BM=
BC=
.
∴∠BOM=60°
∴∠ABE=∠BCE=∠CBE=30°,
∴CF⊥AB
∵∠DCE=90°,
∴DC⊥CF,
∴DC∥AB.
 (1)证明:如图所示,连接DE.
(1)证明:如图所示,连接DE.∵DB垂直BE交圆于点D,∴∠DBE=90°.
∴DE为圆的直径.
∵∠ABC的角平分线BE交圆于点E,
∴
 |
| BE |
 |
| CE |
∴
 |
| DB |
 |
| DC |
∴∠DCB=∠DBC,
∴DB=DC.
(2)解:由(1)可知:∠CDE=∠BDE,DE⊥BC,且平分BC,设中点为M,外接圆的圆心为点O.
连接OB,OC,则OB⊥AB.
在Rt△BOM中,OB=1,BM=
| 1 |
| 2 |
| ||
| 2 |
∴∠BOM=60°
∴∠ABE=∠BCE=∠CBE=30°,
∴CF⊥AB
∵∠DCE=90°,
∴DC⊥CF,
∴DC∥AB.
点评:本题综合考查了圆的切线的性质、同圆中的弧圆周角弦之间的关系、垂径定理及其推论、直角三角形外接圆的性质等基础知识与基本技能方法,考查了推理能力和计算能力,属于基础题.

练习册系列答案
相关题目
甲同学参加一次英语口语考试,已知在备选的10道题中,甲能答对其中的5道题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2道题才算合格.则甲合格的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
等差数列{an}中,若a7-a3=20,则a2014-a2008=( )
| A、40 | B、30 | C、25 | D、20 |
点(1,0)到直线3x+4y-8=0的距离为( )
| A、1 | B、2 | C、3 | D、4 |
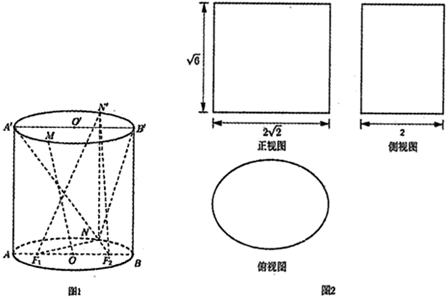
 如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.
如图,四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.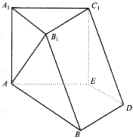 如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.
如图,在六面体A1B1C1D1中,平面A1B1C1∥平面ABDE,△A1B1C1是正三角形,四边形AA1B1B是直角梯形,AB⊥AA1,四边形AEC1A1为正方形,四边形ABDE是等腰梯形,AB∥DE,AB=2AE=2DE=2.