题目内容
如图:四面体P-ABC为正四面体,M为PC的中点,则BM与AC所成的角的余弦值为( ) 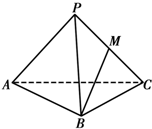

A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:取AP中点N,连结MN,BN,由三角形中位得MN∥AC,从而得到∠BNM是BM与AC所成的角,由此能求出BM与AC所成的角的余弦值.
解答:
 解:取AP中点N,连结MN,BN,
解:取AP中点N,连结MN,BN,
∵M是PC的中点,N是PA的中点,
∴MN∥AC,
∴∠BNM是BM与AC所成的角,
设正四面体P-ABC的棱长为1,
则BN=BM=
=
,MN=
,
∴cos∠BNM=
=
.
∴BM与AC所成的角的余弦值为
.
故选:B.
 解:取AP中点N,连结MN,BN,
解:取AP中点N,连结MN,BN,∵M是PC的中点,N是PA的中点,
∴MN∥AC,
∴∠BNM是BM与AC所成的角,
设正四面体P-ABC的棱长为1,
则BN=BM=
1-
|
| ||
| 2 |
| 1 |
| 2 |
∴cos∠BNM=
| ||||||
2×
|
| ||
| 6 |
∴BM与AC所成的角的余弦值为
| ||
| 6 |
故选:B.
点评:本题考查异面直线所成角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
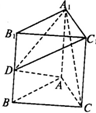 如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )
如图,直三棱柱ABC-A1B1C1中,AB=AC=1,AA1=2,∠B1A1C1=90°,D为BB1的中点,则异面直线C1D与A1C所成角的余弦值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若sin(α+β)=
,sin(α-β)=
,则
等于( )
| 4 |
| 5 |
| 3 |
| 5 |
| tanα |
| tanβ |
| A、7 | ||
| B、-7 | ||
C、
| ||
D、-
|
若(3x-1)7=a7x7+a6x6+…+a1x+a0,则a7+a6+…+a1的值为( )
| A、1 | B、129 |
| C、128 | D、127 |
一份数学试卷由25个选择题构成,每个选择题有4个选项,其中有且仅有1个选项是正确的,每题选正确得4分,不选或选错得0分,满分100分.小强选对任一题的概率为0.8,则他在这次考试中得分的期望为( )
| A、60分 | B、70分 |
| C、80分 | D、90分 |
等差数列{an}中,若a7-a3=20,则a2014-a2008=( )
| A、40 | B、30 | C、25 | D、20 |
一个圆柱的母线长度为2,底为半径为1的圆,则此圆柱的侧面积是( )
| A、π | B、2π | C、3π | D、4π |