题目内容
已知函数f（x）=（2m-3）x2+5mx+7为偶函数，则函数f（x）在（1，4）是（ ）
| A、增函数 |
| B、减函数 |
| C、部分为增函数，部分为减函数 |
| D、无法确定增减性 |
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：利用函数是偶函数，确定函数的解析式与单调性，从而可得结论．
解答：
解：∵函数f（x）=（2m-3）x2+5mx+7为偶函数，
∴f（-x）=f（x），
即（2m-3）x2-5mx+7=（2m-3）x2+5mx+7，
∴m=0
∴f（x）=-3x2+7，
∴f（x）=-3x2+7在（-∞，0）上单调增，在（0，+∞）上单调减，
∴函数f（x）在（1，4）上是减函数，
故选：B．
∴f（-x）=f（x），
即（2m-3）x2-5mx+7=（2m-3）x2+5mx+7，
∴m=0
∴f（x）=-3x2+7，
∴f（x）=-3x2+7在（-∞，0）上单调增，在（0，+∞）上单调减，
∴函数f（x）在（1，4）上是减函数，
故选：B．
点评：本题考查函数的奇偶性与单调性，确定函数的解析式是解题的关键．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
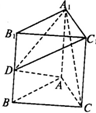如图，直三棱柱ABC-A1B1C1中，AB=AC=1，AA1=2，∠B1A1C1=90°，D为BB1的中点，则异面直线C1D与A1C所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
观察下列各式：
=2
，
=3
，
=4
，…．若
=9
，则n-m=（ ）
2-
|
|
3-
|
|
4-
|
|
9-
|
|
| A、43 | B、57 | C、73 | D、91 |
已知三个球的体积之比为1：8：8，则它们的表面积之比为（ ）
| A、1：2：2 |
| B、1：4：8 |
| C、1：4：4 |
| D、1：8：8 |
甲同学参加一次英语口语考试，已知在备选的10道题中，甲能答对其中的5道题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2道题才算合格．则甲合格的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若sin（α+β）=
，sin（α-β）=
，则
等于（ ）
| 4 |
| 5 |
| 3 |
| 5 |
| tanα |
| tanβ |
| A、7 | ||
| B、-7 | ||
C、
| ||
D、-
|
若（3x-1）7=a7x7+a6x6+…+a1x+a0，则a7+a6+…+a1的值为（ ）
| A、1 | B、129 |
| C、128 | D、127 |