题目内容
已知p:|x-2|≤3,q:
≤0,则p是q的( )
| x+1 |
| x-5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:利用不等式的解法求出,p,q的等价条件,利用充分条件和必要条件的定义即可得到结论.
解答:
解:∵|x-2|≤3,
∴-1≤x≤5,即p:-1≤x≤5,
∵
≤0,
∴-1≤x<5,即q:-1≤x<5,
∴p是q的必要不充分条件.
故选:B.
∴-1≤x≤5,即p:-1≤x≤5,
∵
| x+1 |
| x-5 |
∴-1≤x<5,即q:-1≤x<5,
∴p是q的必要不充分条件.
故选:B.
点评:本题主要考查充分条件和必要条件的判断,利用不等式的解法求出p,q的等价条件是解决本题的关键,比较基础.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
 某几何体的三视图如图所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成,则该几何体的体积为( )
某几何体的三视图如图所示,其侧视图是一个边长为1的等边三角形,俯视图是两个正三角形拼成,则该几何体的体积为( )| A、1 | ||
B、
| ||
C、
| ||
D、
|
 从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为
从甲、乙两个城市分别随机抽取6台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲、乙两组数据的平均数分别为. |
| x |
. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知i为虚数单位,则复数
等于( )
| 2-i |
| 3+i |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知双曲线
-
=1(a,b>0)抛物线y2=4x共焦点,双曲线与抛物线的一公共点到抛物线准线的距离为2,双曲线的离心率为e,则2e-b2的值是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、2
| ||
C、4-2
| ||
| D、4 |
命题“存在x∈R,使得x2+sinx-1≥0”的否定为( )
| A、对任意的x∈R,x2+sinx-1≥0 |
| B、不存在x∈R,使得x2+sinx-1≤0 |
| C、存在x∈R,使得x2+sinx-1<0 |
| D、对任意的x∈R,使得x2+sinx-1<0 |
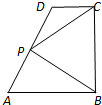 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=2,CD=1,BC=a(a>0),P为线段AD(含端点)上一个动点,设