Question

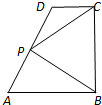如图，在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），P为线段AD（含端点）上一个动点，设

AP

=x

AD

，

PB

•

PC

=y，对于函数y=f（x），给出以下三个结论：
①当a=2时，函数f（x）的值域为[1，4]；
②?a∈（0，+∞），都有f（1）=1成立；
③?a∈（0，+∞），函数f（x）的最大值都等于4．
其中所有正确结论的序号是

 

．

Answer 1

考点：平面向量数量积的运算

专题：平面向量及应用

分析：通过建立如图所示的坐标系，可得y=f（x）=

PB

•

PC

=（a²+1）x²-（4+a²）x+4．x∈[0，1]．
通过分类讨论，利用二次函数的单调性即可判断出．

解答： 解：如图所示，建立直角坐标系．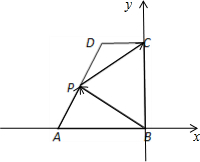
∵在直角梯形ABCD中，AB∥CD，AB⊥BC，AB=2，CD=1，BC=a（a＞0），
∴B（0，0），A（-2，0），D（-1，a），C（0，a）．
∵

AP

=x

AD

，（0≤x≤1）．
∴

BP

=

BA

+x

AD

=（-2，0）+x（1，a）=（x-2，xa），
∴

PC

=

BC

-

BP

=（0，a）-（x-2，xa）=（2-x，a-xa）
∴y=f（x）=

PB

•

PC

=（2-x，-xa）•（2-x，a-xa）
=（2-x）²-ax（a-xa）
=（a²+1）x²-（4+a²）x+4．
①当a=2时，y=f（x）=5x²-8x+4=5(x-

4

5

)2+

4

5

，
∵0≤x≤1，∴当x=

4

5

时，f（x）取得最小值

4

5

；
又f（0）=4，f（1）=1，∴f（x）_max=f（0）=4．
综上可得：函数f（x）的值域为[

4

5

，4]．
因此①不正确．
②由y=f（x）=（a²+1）x²-（4+a²）x+4．
可得：?a∈（0，+∞），都有f（1）=1成立，因此②正确；
③由y=f（x）=（a²+1）x²-（4+a²）x+4．
可知：对称轴x₀=

4+a2

2(a2+1)

．
当0＜a≤

2

时，1＜x₀，∴函数f（x）在[0，1]单调递减，因此当x=0时，函数f（x）取得最大值4．
当a＞

2

时，0＜x₀＜1，函数f（x）在[0，x₀）单调递减，在（x₀，1]上单调递增．
又f（0）=4，f（1）=1，∴f（x）_max=f（0）=4．
因此③正确．
综上可知：只有②③正确．
故答案为：②③．

点评：本题考查了数量积运算、分类讨论、二次函数的单调性等基础知识与基本技能方法，考查了推理能力和计算能力，属于难题．