题目内容
若直角坐标平面内的两不同点P、Q满足条件：①P、Q都在函数y=f（x）的图象上；②P、Q关于原点对称，则称点对[P，Q]是函数y=f（x）的一对“友好点对”（注：点对[P，Q]与[Q，P]看作同一对“友好点对”）．已知函数f（x）=
，则此函数的“友好点对”有（ ）对．
|
| A、0 | B、1 | C、2 | D、3 |
考点：函数的图象,分段函数的应用
专题：函数的性质及应用
分析：根据题意可知只须作出函数y=(
)x（x＞0）的图象关于原点对称的图象，确定它与函数y=-x2-4x（x≤0）交点个数即可．
| 1 |
| 2 |
解答：
解：由题意得：
函数f（x）=
“友好点对”的对数，
等于函数y=(
)x（x＞0）的图象关于原点对称的图象，与函数y=-x2-4x（x≤0）交点个数
在同一坐标系中做出函数y=(
)x（x＞0）的图象关于原点对称的图象，与函数y=-x2-4x（x≤0）的图象如下图所示：
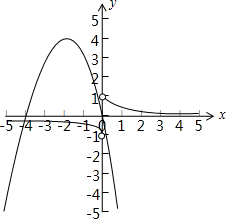
由图象可知，两个图象只有一个交点．
故选B
函数f（x）=
|
等于函数y=(
| 1 |
| 2 |
在同一坐标系中做出函数y=(
| 1 |
| 2 |
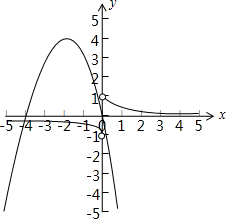
由图象可知，两个图象只有一个交点．
故选B
点评：本题考查的知识点是函数的图象，分段函数，新定义，其中将“友好点对”的对数转化为对应图象交点个数是解答的关键．
练习册系列答案
相关题目
已知p：|x-2|≤3，q：
≤0，则p是q的（ ）
| x+1 |
| x-5 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若集合A={y|y=ax，a＞0，x≠1}，则∁RA等于（ ）
| A、（-∞，0） |
| B、（-∞，0] |
| C、（0，+∞） |
| D、[0，+∞） |
已知直线3x+4y-5=0与圆x2+y2=4相交于A，B两点，那么弦AB的长等于（ ）
A、3
| ||
B、2
| ||
C、
| ||
| D、1 |
证明：card（A∪B∪C）=card（A）+card（B）+card（C）-card（A∩B）-card（A∩C）-card（B∩C）+card（A∩B∩C）